Последние темы
» Вити больше нет!автор bug19 Пн Фев 20 2023, 19:54
» Собираем оригинальный Орион 128
автор bug19 Пн Фев 20 2023, 19:47
» Проблема плющеного экрана ОРИОНА
автор kanzler Пн Ноя 28 2022, 12:05
» Орион 128 и его клоны возрождение 2019-2022 год
автор kanzler Пн Ноя 28 2022, 12:03
» Электроника КР-04. Информация, документы, фото.
автор kanzler Пн Ноя 28 2022, 12:02
» Новости форума
автор kanzler Пн Ноя 28 2022, 11:52
» Орион-128 НГМД запуск 2021 года
автор matrixplus Сб Сен 10 2022, 17:36
» ПЗУ F800 для РК86
автор ведущий_специалист Сб Сен 10 2022, 10:37
» Микропроцессорная лаборатория "Микролаб К580ИК80", УМК-80, УМПК-80 и др.
автор Электротехник Вт Июл 26 2022, 19:33
» Орион-128 SD карта в Орионе
автор matrixplus Чт Июн 02 2022, 09:00
» 7 Мая. День Радио!
автор Viktor2312 Чт Май 12 2022, 10:58
» Серия: Массовая радио библиотека. МРБ
автор Viktor2312 Ср Май 11 2022, 12:17
» Полезные книги
автор Viktor2312 Пн Май 09 2022, 15:07
» Орион 128 Стандарты портов и системной шины Х2
автор matrixplus Вс Май 08 2022, 23:08
» Орион-128 и Орион ПРО еще раз про блоки питания
автор matrixplus Вс Май 08 2022, 19:09
» Орион-128 Программаторы
автор matrixplus Вс Май 08 2022, 19:02
» Орион ПРО история сборки 2021 до 2022
автор matrixplus Вс Май 08 2022, 18:47
» Анонсы монет (New coin).
автор Viktor2312 Сб Май 07 2022, 23:11
» Хочу свой усилок для квартиры собрать не спеша
автор Viktor2312 Сб Май 07 2022, 19:33
» Амфитон 25у-002С
автор Viktor2312 Сб Май 07 2022, 09:38
» Майнер: T-Rex
автор Viktor2312 Вс Май 01 2022, 09:12
» GoWin. Изучение документации. SUG100-2.6E_Gowin Software User Guide. Среда разработки EDA.
автор Viktor2312 Пн Апр 25 2022, 01:01
» GoWin. Изучение документации. UG286-1.9.1E Gowin Clock User Guide.
автор Viktor2312 Сб Апр 23 2022, 18:22
» GoWin. Documentation Database. Device. GW2A.
автор Viktor2312 Ср Апр 20 2022, 14:08
» GOWIN AEC IP
автор Viktor2312 Ср Апр 20 2022, 12:08
Самые активные пользователи за месяц
| Нет пользователей |
Поиск
Языки программирования. Статьи, заметки, очерки, разное...
Страница 1 из 1 • Поделиться
 Языки программирования. Статьи, заметки, очерки, разное...
Языки программирования. Статьи, заметки, очерки, разное...
1
.
Программист-самоучка из Бельгии решил 20-летнюю криптографическую задачку из MIT.
Задачу в 1999 году придумал Рональд Ривест, профессор Лаборатории искусственного интеллекта MIT и один из создателей криптографического алгоритма RSA. Сама по себе она не преследует никаких научных целей. Однако решать её нужно сугубо последовательными вычислениями, поэтому её создатель думал, что она решится не раньше 2034 года.
Задачка:
Description of the LCS35 Time Capsule Crypto-Puzzle
by Ronald L. Rivest
April 4, 1999
As part of the celebration of the 35th birthday of MIT's Laboratory
for Computer Science, LCS Director Michael Dertouzos will present an
"LCS Time Capsule of Innovations" to architect Frank Gehry. The Time
Capsule will reside in the new building, designed by Gehry, that will
house LCS. The time capsule will be unsealed on the earlier of 70
years from the inception of the Laboratory (on or about 2033), or upon
solution of a cryptographic puzzle, described herein. This puzzle is
designed to take approximately 35 years to solve. It uses the ideas
described in the paper
"Time-lock puzzles and timed-release Crypto"
by myself, Adi Shamir, and David Wagner. A copy of this paper can be
found at http://theory.lcs.mit.edu/~rivest/RivestShamirWagner-timelock.ps.
The puzzle is designed to foil attempts of a solver to exploit
parallel or distributed computing to speed up the computation. The
computation required to solve the puzzle is "intrinsically
sequential".
The problem is to compute 2^(2^t) (mod n) for specified values of t
and n. Here n is the product of two large primes, and t is chosen to
set the desired level of difficulty of the puzzle.
Note that the puzzle can be solved by performing t successive
squarings modulo n, beginning with the value 2. That is, set
W(0) = 2
W(i+1) = (W(i)^2) (mod n) for i>0,
and compute W(t). There is no known way to perform this computation
more quickly without knowing the factorization of n.
The value of t was chosen to take into consideration the growth in
computational power due to "Moore's Law". Based on the SEMATECH
National Technology Roadmap for Semiconductors (1997 edition), we can
expect internal chip speeds to increase by a factor of approximately
13 overall up to 2012, when the clock rates reach about 10GHz. After
that improvements seem more difficult, but we estimate that another
factor of five might be achievable by 2034. Thus, the overall rate of
computation should go through approximately six doublings by 2034.
We estimate that the puzzle will require 35 years of continuous
computation to solve, with the computer being replaced every year by
the next fastest model available. Most of the work will really be
done in the last few years, however.
An interesting question is how to protect such a computation from
errors. If you have an error in year 3 that goes undetected, you may
waste the next 32 years of computing. Adi Shamir has proposed a slick
means of checking your computation as you go, as follows. Pick a
small (50-bit) prime c, and perform the computation modulo cn rather
than just modulo n. You can check the result modulo c whenever you
like; this should be a extremely effective check on the computation
modulo n as well.
In order to allow the LCS director in the year 2034 (or whenever) to
verify a submitted solution, we have arranged things so that solving
the puzzle also enables the solver to factor the modulus n, as
described below.
Of course, one way to break the puzzle is to factor the modulus n
directly. But we have chosen a 2048-bit modulus, which is unlikely to
be factored in the given time frame without a breakthrough in the art
of factoring. Just as a failure of Moore's Law could make the puzzle
harder than intended, a breakthrough in the art of factoring would
make the puzzle easier than intended.
Here is a smaller example of the puzzle.
Suppose n = 11*23 = 253, and t = 10. Then we can compute:
2^(2^1) = 2^2 = 4 (mod 253)
2^(2^2) = 4^2 = 16 (mod 253)
2^(2^3) = 16^2 = 3 (mod 253)
2^(2^4) = 3^2 = 9 (mod 253)
2^(2^5) = 9^2 = 81 (mod 253)
2^(2^6) = 81^2 = 236 (mod 253)
2^(2^7) = 236^2 = 36 (mod 253)
2^(2^8 ) = 36^2 = 31 (mod 253)
2^(2^9) = 31^2 = 202 (mod 253)
w = 2^(2^t) = 2^(2^10) = 202^2 = 71 (mod 253)
Thus, the "w" value computed for the puzzle is 71 (decimal), which is
47 (hex). If we have a "z" value for the puzzle of 13 (hex), then the
"secret message" for the example is (47 xor 13) = 54 (hex). (The secret
message should then be interpreted in ascii at 8 bits per character.)
Attached below is the Java code for generating the puzzle, and the
actual puzzle itself.
Anyone who believes to have solved the puzzle, should submit the resultant
English sentence along with the factorization of n and relevant solution
notes to the Director of LCS. Upon verification of the solution, the LCS
Director will unseal the capsule at a ceremony set up for that purpose. If
no solution is established by September 2033, then the LCS Director will
unseal the capsule at the Laboratory's 70th anniversary celebration, or at
a suitable alternate event. In the absence of an LCS Director, the
President of MIT will designate another official or individual.
Good luck!
(Thanks to Scott Contini, Dimitri Antoniadis, Tom Knight, Steve
Senturia, Adi Shamir, David Wagner, and Michael Dertouzos for their
assistance!)
==============================================================================
/* Program to create "Time-Lock Puzzle" for LCS35 Time Capsule
Ronald L. Rivest
April 2, 1999
*/
import java.io.*;
import java.util.Random;
import java.math.BigInteger;
import java.lang.Math;
public class TimeLockPuzzle {
public TimeLockPuzzle () {}
static BufferedReader in = new BufferedReader(new InputStreamReader(System.in));
static public void main(String args[]) throws IOException {
System.out.println("Creating LCS35 Time Capsule Crypto-Puzzle...");
CreatePuzzle();
System.out.println("Puzzle Created.");
}
static public void CreatePuzzle() throws IOException {
// Compute count of squarings to do each year
BigInteger squaringsPerSecond = new BigInteger("3000"); // in 1999
System.out.println("Assumed number of squarings/second (now) = "+
squaringsPerSecond);
BigInteger secondsPerYear = new BigInteger("31536000");
BigInteger squaringsFirstYear = secondsPerYear.multiply(squaringsPerSecond);
System.out.println("Squarings (first year) = "+squaringsFirstYear);
int years = 35;
BigInteger t = new BigInteger("0");
BigInteger s = squaringsFirstYear;
for (int i = 1999;i<=1998+years;i++)
{ // do s squarings in year i
t = t.add(s);
// apply Moore's Law to get number of squarings to do the next year
String growth = new String("");
growth = "12204"; // ~x13 up to 2012, at constant rate
if (i>2012) growth = "10750"; // ~x5 up to 2034, at constant rate
s = s.multiply(new BigInteger(growth)).divide(new BigInteger("10000"));
}
System.out.println("Squarings (total)= " + t);
System.out.println("Ratio of total to first year = "+
t.divide(squaringsFirstYear));
System.out.println("Ratio of last year to first year = "+
s.divide(squaringsFirstYear.multiply(new BigInteger("10758"))
.divide(new BigInteger("10000"))));
// Now generate RSA parameters
int primelength = 1024;
System.out.println("Using "+primelength+"-bit primes.");
BigInteger twoPower = (new BigInteger("1")).shiftLeft(primelength);
String pseed = getString("large random integer for prime p seed");
BigInteger prand = new BigInteger(pseed);
String qseed = getString("large random integer for prime q seed");
BigInteger qrand = new BigInteger(qseed);
System.out.println("Computing...");
BigInteger p = new BigInteger("5");
// Note that 5 has maximal order modulo 2^k (See Knuth)
p = getNextPrime(p.modPow(prand,twoPower));
System.out.println("p = "+p);
BigInteger q = new BigInteger("5");
q = getNextPrime(q.modPow(qrand,twoPower));
System.out.println("q = "+q);
BigInteger n = p.multiply(q);
System.out.println("n = "+n);
BigInteger pm1 = p.subtract(ONE);
BigInteger qm1 = q.subtract(ONE);
BigInteger phi = pm1.multiply(qm1);
System.out.println("phi = "+phi);
// Now generate final puzzle value w
BigInteger u = TWO.modPow(t,phi);
BigInteger w = TWO.modPow(u,n);
System.out.println("w (hex) = "+w.toString(16));
// Obtain and encrypt the secret message
// Include seed for p as a check
StringBuffer sgen = new StringBuffer(getString("string for secret"));
sgen = sgen.append(" (seed value b for p = "+prand.toString()+")");
System.out.println("Puzzle secret = "+sgen);
BigInteger secret = getBigIntegerFromStringBuffer(sgen);
if (secret.compareTo(n) > 0)
{ System.out.println("Secret too large!"); return; }
BigInteger z = secret.xor(w);
System.out.println("z(hex) = "+z.toString(16));
// Write output to a file
PrintWriter pw = new PrintWriter(new FileWriter("C:\\puzzleoutput.txt"));
pw.println("Crypto-Puzzle for LCS35 Time Capsule.");
pw.println("Created by Ronald L. Rivest. April 2, 1999."); pw.println();
pw.println("Puzzle parameters (all in decimal):"); pw.println();
pw.print("n = "); printBigInteger(n,pw); pw.println();
pw.print("t = "); printBigInteger(t,pw); pw.println();
pw.print("z = "); printBigInteger(z,pw); pw.println();
pw.println("To solve the puzzle, first compute w = 2^(2^t) (mod n).");
pw.println("Then exclusive-or the result with z.");
pw.println("(Right-justify the two strings first.)");
pw.println();
pw.println("The result is the secret message (8 bits per character),");
pw.println("including information that will allow you to factor n.");
pw.println("(The extra information is a seed value b, such that ");
pw.println("5^b (mod 2^1024) is just below a prime factor of n.)");
pw.println(" ");
pw.close();
// Wait for input carriage return to pause before closing
System.in.read();
}
final static BigInteger ONE = new BigInteger("1");
final static BigInteger TWO = new BigInteger("2");
static String getString(String what) throws IOException {
// This routine is essentially a prompted "readLine"
StringBuffer s = new StringBuffer();
System.out.println("Enter "+what+" followed by a carriage return:");
for (int i = 0;i<1000;i++)
{ int c = System.in.read();
if (c<0 || c == '\n') break;
if (c != '\r') // note: ignore cr before newline
s = s.append((char)c);
}
return(s.toString());
}
static BigInteger getBigIntegerFromStringBuffer(StringBuffer s)
throws IOException {
// Base-256 interpretation of the given string
BigInteger randbi = new BigInteger("0");
for (int i = 0;i<s.length();i++)
{ int c = s.charAt(i);
randbi = randbi.shiftLeft( 8 ).add(new BigInteger(Integer.toString(c)));
}
System.out.println("Value of string entered (hex) = "+randbi.toString(16));
return randbi;
}
static void printBigInteger (BigInteger x, PrintWriter pw) {
String s = x.toString();
int charsPerLine = 60;
for (int i = 0;i<s.length();i+=charsPerLine)
{ if (i!=0) { pw.println(); pw.print(" "); }
pw.print(s.substring(i,java.lang.Math.min(i+charsPerLine,s.length())));
}
pw.println();
}
static BigInteger getNextPrime(BigInteger startvalue)
{
BigInteger p = startvalue;
if (!p.and(ONE).equals(ONE)) p = p.add(ONE);
while (!p.isProbablePrime(40)) p = p.add(TWO);
return(p);
}
}// end of TimeLockPuzzle class
==============================================================================
Crypto-Puzzle for LCS35 Time Capsule.
Created by Ronald L. Rivest. April 2, 1999.
Puzzle parameters (all in decimal):
n = 631446608307288889379935712613129233236329881833084137558899
077270195712892488554730844605575320651361834662884894808866
350036848039658817136198766052189726781016228055747539383830
826175971321892666861177695452639157012069093997368008972127
446466642331918780683055206795125307008202024124623398241073
775370512734449416950118097524189066796385875485631980550727
370990439711973361466670154390536015254337398252457931357531
765364633198906465140213398526580034199190398219284471021246
488745938885358207031808428902320971090703239693491996277899
532332018406452247646396635593736700936921275809208629319872
7008292431243681
t = 79685186856218
z = 427338526681239414707099486152541907807623930474842759553127
699575212802021361367225451651600353733949495680760238284875
258690199022379638588291839885522498545851997481849074579523
880422628363751913235562086585480775061024927773968205036369
669785002263076319003533000450157772067087172252728016627835
400463807389033342175518988780339070669313124967596962087173
533318107116757443584187074039849389081123568362582652760250
029401090870231288509578454981440888629750522601069337564316
940360631375375394366442662022050529545706707758321979377282
989361374561414204719371297211725179287931039547753581030226
7611143659071382
To solve the puzzle, first compute w = 2^(2^t) (mod n).
Then exclusive-or the result with z.
(Right-justify the two strings first.)
The result is the secret message (8 bits per character),
including information that will allow you to factor n.
(The extra information is a seed value b, such that
5^b (mod 2^1024) is just below a prime factor of n.)
==============================================================================
MIT
Программист-самоучка из Бельгии решил 20-летнюю криптографическую задачку из MIT.
Задачу в 1999 году придумал Рональд Ривест, профессор Лаборатории искусственного интеллекта MIT и один из создателей криптографического алгоритма RSA. Сама по себе она не преследует никаких научных целей. Однако решать её нужно сугубо последовательными вычислениями, поэтому её создатель думал, что она решится не раньше 2034 года.
Задачка:
Description of the LCS35 Time Capsule Crypto-Puzzle
by Ronald L. Rivest
April 4, 1999
As part of the celebration of the 35th birthday of MIT's Laboratory
for Computer Science, LCS Director Michael Dertouzos will present an
"LCS Time Capsule of Innovations" to architect Frank Gehry. The Time
Capsule will reside in the new building, designed by Gehry, that will
house LCS. The time capsule will be unsealed on the earlier of 70
years from the inception of the Laboratory (on or about 2033), or upon
solution of a cryptographic puzzle, described herein. This puzzle is
designed to take approximately 35 years to solve. It uses the ideas
described in the paper
"Time-lock puzzles and timed-release Crypto"
by myself, Adi Shamir, and David Wagner. A copy of this paper can be
found at http://theory.lcs.mit.edu/~rivest/RivestShamirWagner-timelock.ps.
The puzzle is designed to foil attempts of a solver to exploit
parallel or distributed computing to speed up the computation. The
computation required to solve the puzzle is "intrinsically
sequential".
The problem is to compute 2^(2^t) (mod n) for specified values of t
and n. Here n is the product of two large primes, and t is chosen to
set the desired level of difficulty of the puzzle.
Note that the puzzle can be solved by performing t successive
squarings modulo n, beginning with the value 2. That is, set
W(0) = 2
W(i+1) = (W(i)^2) (mod n) for i>0,
and compute W(t). There is no known way to perform this computation
more quickly without knowing the factorization of n.
The value of t was chosen to take into consideration the growth in
computational power due to "Moore's Law". Based on the SEMATECH
National Technology Roadmap for Semiconductors (1997 edition), we can
expect internal chip speeds to increase by a factor of approximately
13 overall up to 2012, when the clock rates reach about 10GHz. After
that improvements seem more difficult, but we estimate that another
factor of five might be achievable by 2034. Thus, the overall rate of
computation should go through approximately six doublings by 2034.
We estimate that the puzzle will require 35 years of continuous
computation to solve, with the computer being replaced every year by
the next fastest model available. Most of the work will really be
done in the last few years, however.
An interesting question is how to protect such a computation from
errors. If you have an error in year 3 that goes undetected, you may
waste the next 32 years of computing. Adi Shamir has proposed a slick
means of checking your computation as you go, as follows. Pick a
small (50-bit) prime c, and perform the computation modulo cn rather
than just modulo n. You can check the result modulo c whenever you
like; this should be a extremely effective check on the computation
modulo n as well.
In order to allow the LCS director in the year 2034 (or whenever) to
verify a submitted solution, we have arranged things so that solving
the puzzle also enables the solver to factor the modulus n, as
described below.
Of course, one way to break the puzzle is to factor the modulus n
directly. But we have chosen a 2048-bit modulus, which is unlikely to
be factored in the given time frame without a breakthrough in the art
of factoring. Just as a failure of Moore's Law could make the puzzle
harder than intended, a breakthrough in the art of factoring would
make the puzzle easier than intended.
Here is a smaller example of the puzzle.
Suppose n = 11*23 = 253, and t = 10. Then we can compute:
2^(2^1) = 2^2 = 4 (mod 253)
2^(2^2) = 4^2 = 16 (mod 253)
2^(2^3) = 16^2 = 3 (mod 253)
2^(2^4) = 3^2 = 9 (mod 253)
2^(2^5) = 9^2 = 81 (mod 253)
2^(2^6) = 81^2 = 236 (mod 253)
2^(2^7) = 236^2 = 36 (mod 253)
2^(2^8 ) = 36^2 = 31 (mod 253)
2^(2^9) = 31^2 = 202 (mod 253)
w = 2^(2^t) = 2^(2^10) = 202^2 = 71 (mod 253)
Thus, the "w" value computed for the puzzle is 71 (decimal), which is
47 (hex). If we have a "z" value for the puzzle of 13 (hex), then the
"secret message" for the example is (47 xor 13) = 54 (hex). (The secret
message should then be interpreted in ascii at 8 bits per character.)
Attached below is the Java code for generating the puzzle, and the
actual puzzle itself.
Anyone who believes to have solved the puzzle, should submit the resultant
English sentence along with the factorization of n and relevant solution
notes to the Director of LCS. Upon verification of the solution, the LCS
Director will unseal the capsule at a ceremony set up for that purpose. If
no solution is established by September 2033, then the LCS Director will
unseal the capsule at the Laboratory's 70th anniversary celebration, or at
a suitable alternate event. In the absence of an LCS Director, the
President of MIT will designate another official or individual.
Good luck!
(Thanks to Scott Contini, Dimitri Antoniadis, Tom Knight, Steve
Senturia, Adi Shamir, David Wagner, and Michael Dertouzos for their
assistance!)
==============================================================================
/* Program to create "Time-Lock Puzzle" for LCS35 Time Capsule
Ronald L. Rivest
April 2, 1999
*/
import java.io.*;
import java.util.Random;
import java.math.BigInteger;
import java.lang.Math;
public class TimeLockPuzzle {
public TimeLockPuzzle () {}
static BufferedReader in = new BufferedReader(new InputStreamReader(System.in));
static public void main(String args[]) throws IOException {
System.out.println("Creating LCS35 Time Capsule Crypto-Puzzle...");
CreatePuzzle();
System.out.println("Puzzle Created.");
}
static public void CreatePuzzle() throws IOException {
// Compute count of squarings to do each year
BigInteger squaringsPerSecond = new BigInteger("3000"); // in 1999
System.out.println("Assumed number of squarings/second (now) = "+
squaringsPerSecond);
BigInteger secondsPerYear = new BigInteger("31536000");
BigInteger squaringsFirstYear = secondsPerYear.multiply(squaringsPerSecond);
System.out.println("Squarings (first year) = "+squaringsFirstYear);
int years = 35;
BigInteger t = new BigInteger("0");
BigInteger s = squaringsFirstYear;
for (int i = 1999;i<=1998+years;i++)
{ // do s squarings in year i
t = t.add(s);
// apply Moore's Law to get number of squarings to do the next year
String growth = new String("");
growth = "12204"; // ~x13 up to 2012, at constant rate
if (i>2012) growth = "10750"; // ~x5 up to 2034, at constant rate
s = s.multiply(new BigInteger(growth)).divide(new BigInteger("10000"));
}
System.out.println("Squarings (total)= " + t);
System.out.println("Ratio of total to first year = "+
t.divide(squaringsFirstYear));
System.out.println("Ratio of last year to first year = "+
s.divide(squaringsFirstYear.multiply(new BigInteger("10758"))
.divide(new BigInteger("10000"))));
// Now generate RSA parameters
int primelength = 1024;
System.out.println("Using "+primelength+"-bit primes.");
BigInteger twoPower = (new BigInteger("1")).shiftLeft(primelength);
String pseed = getString("large random integer for prime p seed");
BigInteger prand = new BigInteger(pseed);
String qseed = getString("large random integer for prime q seed");
BigInteger qrand = new BigInteger(qseed);
System.out.println("Computing...");
BigInteger p = new BigInteger("5");
// Note that 5 has maximal order modulo 2^k (See Knuth)
p = getNextPrime(p.modPow(prand,twoPower));
System.out.println("p = "+p);
BigInteger q = new BigInteger("5");
q = getNextPrime(q.modPow(qrand,twoPower));
System.out.println("q = "+q);
BigInteger n = p.multiply(q);
System.out.println("n = "+n);
BigInteger pm1 = p.subtract(ONE);
BigInteger qm1 = q.subtract(ONE);
BigInteger phi = pm1.multiply(qm1);
System.out.println("phi = "+phi);
// Now generate final puzzle value w
BigInteger u = TWO.modPow(t,phi);
BigInteger w = TWO.modPow(u,n);
System.out.println("w (hex) = "+w.toString(16));
// Obtain and encrypt the secret message
// Include seed for p as a check
StringBuffer sgen = new StringBuffer(getString("string for secret"));
sgen = sgen.append(" (seed value b for p = "+prand.toString()+")");
System.out.println("Puzzle secret = "+sgen);
BigInteger secret = getBigIntegerFromStringBuffer(sgen);
if (secret.compareTo(n) > 0)
{ System.out.println("Secret too large!"); return; }
BigInteger z = secret.xor(w);
System.out.println("z(hex) = "+z.toString(16));
// Write output to a file
PrintWriter pw = new PrintWriter(new FileWriter("C:\\puzzleoutput.txt"));
pw.println("Crypto-Puzzle for LCS35 Time Capsule.");
pw.println("Created by Ronald L. Rivest. April 2, 1999."); pw.println();
pw.println("Puzzle parameters (all in decimal):"); pw.println();
pw.print("n = "); printBigInteger(n,pw); pw.println();
pw.print("t = "); printBigInteger(t,pw); pw.println();
pw.print("z = "); printBigInteger(z,pw); pw.println();
pw.println("To solve the puzzle, first compute w = 2^(2^t) (mod n).");
pw.println("Then exclusive-or the result with z.");
pw.println("(Right-justify the two strings first.)");
pw.println();
pw.println("The result is the secret message (8 bits per character),");
pw.println("including information that will allow you to factor n.");
pw.println("(The extra information is a seed value b, such that ");
pw.println("5^b (mod 2^1024) is just below a prime factor of n.)");
pw.println(" ");
pw.close();
// Wait for input carriage return to pause before closing
System.in.read();
}
final static BigInteger ONE = new BigInteger("1");
final static BigInteger TWO = new BigInteger("2");
static String getString(String what) throws IOException {
// This routine is essentially a prompted "readLine"
StringBuffer s = new StringBuffer();
System.out.println("Enter "+what+" followed by a carriage return:");
for (int i = 0;i<1000;i++)
{ int c = System.in.read();
if (c<0 || c == '\n') break;
if (c != '\r') // note: ignore cr before newline
s = s.append((char)c);
}
return(s.toString());
}
static BigInteger getBigIntegerFromStringBuffer(StringBuffer s)
throws IOException {
// Base-256 interpretation of the given string
BigInteger randbi = new BigInteger("0");
for (int i = 0;i<s.length();i++)
{ int c = s.charAt(i);
randbi = randbi.shiftLeft( 8 ).add(new BigInteger(Integer.toString(c)));
}
System.out.println("Value of string entered (hex) = "+randbi.toString(16));
return randbi;
}
static void printBigInteger (BigInteger x, PrintWriter pw) {
String s = x.toString();
int charsPerLine = 60;
for (int i = 0;i<s.length();i+=charsPerLine)
{ if (i!=0) { pw.println(); pw.print(" "); }
pw.print(s.substring(i,java.lang.Math.min(i+charsPerLine,s.length())));
}
pw.println();
}
static BigInteger getNextPrime(BigInteger startvalue)
{
BigInteger p = startvalue;
if (!p.and(ONE).equals(ONE)) p = p.add(ONE);
while (!p.isProbablePrime(40)) p = p.add(TWO);
return(p);
}
}// end of TimeLockPuzzle class
==============================================================================
Crypto-Puzzle for LCS35 Time Capsule.
Created by Ronald L. Rivest. April 2, 1999.
Puzzle parameters (all in decimal):
n = 631446608307288889379935712613129233236329881833084137558899
077270195712892488554730844605575320651361834662884894808866
350036848039658817136198766052189726781016228055747539383830
826175971321892666861177695452639157012069093997368008972127
446466642331918780683055206795125307008202024124623398241073
775370512734449416950118097524189066796385875485631980550727
370990439711973361466670154390536015254337398252457931357531
765364633198906465140213398526580034199190398219284471021246
488745938885358207031808428902320971090703239693491996277899
532332018406452247646396635593736700936921275809208629319872
7008292431243681
t = 79685186856218
z = 427338526681239414707099486152541907807623930474842759553127
699575212802021361367225451651600353733949495680760238284875
258690199022379638588291839885522498545851997481849074579523
880422628363751913235562086585480775061024927773968205036369
669785002263076319003533000450157772067087172252728016627835
400463807389033342175518988780339070669313124967596962087173
533318107116757443584187074039849389081123568362582652760250
029401090870231288509578454981440888629750522601069337564316
940360631375375394366442662022050529545706707758321979377282
989361374561414204719371297211725179287931039547753581030226
7611143659071382
To solve the puzzle, first compute w = 2^(2^t) (mod n).
Then exclusive-or the result with z.
(Right-justify the two strings first.)
The result is the secret message (8 bits per character),
including information that will allow you to factor n.
(The extra information is a seed value b, such that
5^b (mod 2^1024) is just below a prime factor of n.)
==============================================================================
Последний раз редактировалось: Viktor2312 (Пн Янв 13 2020, 13:14), всего редактировалось 1 раз(а)
Viktor2312- RIP
- Сообщения : 15492
Дата регистрации : 2012-08-10
Возраст : 45
Откуда : Пятигорск
 Re: Языки программирования. Статьи, заметки, очерки, разное...
Re: Языки программирования. Статьи, заметки, очерки, разное...
2
.
____Вышел первый в 2020 году рейтинг языков программирования TIOBE. Лидеры уже который месяц неизменны — это Java (1-е место), за ним Си, Python и C++. Языком 2019 года стал, как ни странно, не Python, а Си. У экспертов есть тому логичное объяснение.
____По мнению специалистов, в растущей популярности Си большое значение имеет развитие Интернета вещей (IoT). Язык хорошо ложится на небольшие устройства, для которых важна производительность. Таких устройств на рынке становится всё больше — всё чаще разработчики обращаются к Си. В 2018 году звание языка года получил Python — в третий раз за историю TIOBE, такого ни у одного языка не было. Теперь то же достижение повторил Си. Он получил награды в 2008, 2017 и теперь в 2019 году.
.
Язык года. Кратко.
____Вышел первый в 2020 году рейтинг языков программирования TIOBE. Лидеры уже который месяц неизменны — это Java (1-е место), за ним Си, Python и C++. Языком 2019 года стал, как ни странно, не Python, а Си. У экспертов есть тому логичное объяснение.
____По мнению специалистов, в растущей популярности Си большое значение имеет развитие Интернета вещей (IoT). Язык хорошо ложится на небольшие устройства, для которых важна производительность. Таких устройств на рынке становится всё больше — всё чаще разработчики обращаются к Си. В 2018 году звание языка года получил Python — в третий раз за историю TIOBE, такого ни у одного языка не было. Теперь то же достижение повторил Си. Он получил награды в 2008, 2017 и теперь в 2019 году.
***
.
Viktor2312- RIP
- Сообщения : 15492
Дата регистрации : 2012-08-10
Возраст : 45
Откуда : Пятигорск
 Re: Языки программирования. Статьи, заметки, очерки, разное...
Re: Языки программирования. Статьи, заметки, очерки, разное...
3
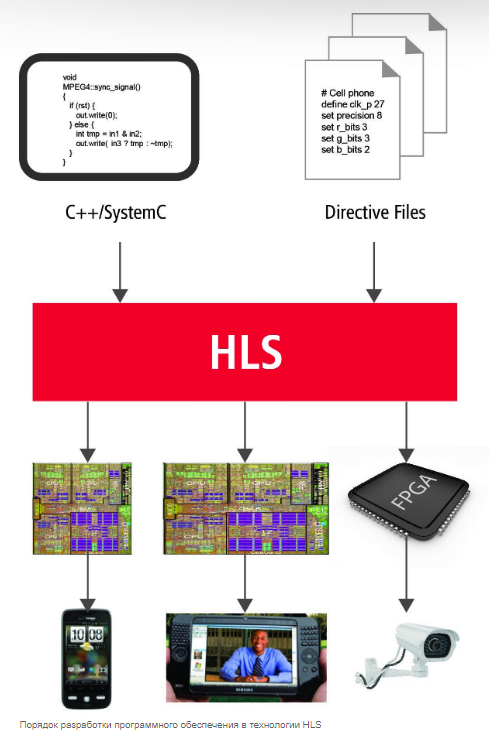
Программирование будущего называется HLS.
Ещё в 80-х годах прошлого столетия в области разработки цифровых устройств начали применяться специализированные языки проектирования, называемые ещё языками описания аппаратуры или HDL языки. Наиболее широкое распространение получили VHDL и Verilog. Эти замечательные языки позволяют вести разработку цифровых схем как на самом низком уровне, работая с отдельными вентилями, и иногда даже с транзисторами, так и на самом высоком структурном уровне.
Такое полезное свойство интегральных схем, как высокая производительность постепенно выходит на самый первый план. В идеальных представлениях фундаментальные алгоритмы, описанные на языках Си и С++, являющиеся сердцем высоко-нагруженных приложений должны быть без особых доработок преобразованы в максимально быстродействующие схемы, способные быстро, желательно за один такт, получать нужный результат вычислений. Такие схемы должны быть очень эффективно разложены на ресурсы ПЛИС.
Краткий обзор технологии HLS.
Как дела обстоят сейчас? Можно ли напрямую перенести алгоритмы на ПЛИС? Что этому мешает и какова реально занимаемая новой технологией ниша?
В настоящий момент Xilinx и Intel как два задающих моду производителя рассматривают языки Си и С++ в качестве инструмента переноса алгоритмов в новый мир параллельных вычислений. Это обосновано тем, что за более чем 45 лет существования языка Си, на нём написаны практически все известные алгоритмы и конечно же все самые важные и фундаментальные из них.
В простом процессоре для вычислений выделяется одно арифметико-логическое устройство. Так вот, чтобы прийти к конечному решению, мы настроили своё сознание так чтобы разложить все вычисления на конечное число простых операций. Выполняя их в строго определенном порядке, процессор придёт к решению задачи. Это всё именуют алгоритмом.
Правильный порядок выполнения операций процессором достигается слаженной работой массы специальных модулей. Это флаги выполнения операций, дешифратор команд, управляющий направлением данных к тому или иному узлу процессора. Выполнение функции сопровождается передачей параметров через стек, сохранением адреса возврата, размещением в стеке локальных переменных. Это всё приводит ко многим машинным инструкциям, на которые уходят бесчисленные такты процессора и соответственно большое количество времени.
Теперь же в новой параллельной вселенной всё будет совсем не так. Больше нет такой вольности, как бесчисленное количество тактов.
Время теперь это наиболее ценный ресурс.
Чтобы обеспечить максимально параллельное и быстрое выполнение вычислений, в нашем распоряжении большое число ресурсов ПЛИС, буквально утопающих в матрице коммутации. И с этим всем хозяйством необходимо обращаться крайне разумно и осторожно. Давайте на простых примерах посмотрим сколько новой информации необходимо иметь ввиду простому программисту, чтобы используя традиционный язык программирования очень коротко и точно выразить свою мысль системе проектирования.
Кто есть кто теперь?
Итак, функции это теперь не размещение аргументов и переменных в стеке. Стека теперь вообще не существует. Функция это самостоятельный блок, на вход которого приходят параметры.
В этом примере на входе 4 шины данных. На выходной шине данных появится результат. Для выполнения всех операций достаточно одного умножителя и одного сумматора. Если иметь два сумматора, то функция выполнится максимально быстро, но при этом будет задействовано максимальное количество ресурсов. Компромиссный вариант потребует одного сумматора и результат выполнения функции появится на втором такте.
Один и тот же сумматор на первом такте сработает в операции суммы произведения с числом b, результат будет записан в регистр, изображенный зелёным цветом. На втором такте произойдёт сумма промежуточного результата, с числом c. На вход сумматора будут поданы совсем другие слагаемые. Это довольно легко решается при помощи мультиплексора, но естественно вносит дополнительную задержку.
Даже на таком простом примере видно, что можно довольно гибко управлять производительностью вычислительного процесса и подбирать компромиссные решения. Обычный программист, приходящий в эту область должен хорошо представлять все возможные варианты и какими средствами ими можно управлять.
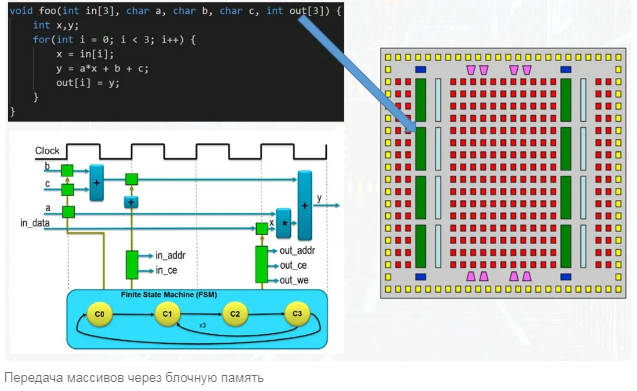
Теперь пример немного сложнее.
На входе функции имеются массивы чисел, один входной и один выходной. Кроме того, в теле функции присутствует цикл. Если подходить к решению задачи с позиции экономии ресурсов, распараллеливается тело цикла, но каждая итерация приводит к повторному использованию всё тех же сумматоров и умножителей. Итеративное выполнение обеспечивает такой механизм, как автомат состояний.
Теперь необходимо отметить, что массивы данных передаются от функции к функции через блоки памяти.
Это один из основных ресурсов ПЛИС, позволяющий вести одновременную запись и чтение. Этому способствует наличие двух независимых комплектов шин и управляющих линий блочной памяти. За один такт можно считать или записать только одну ячейку данных. Доступ к ячейкам осуществляется отдельным механизмом вычисления адреса, работа которого контролируется при помощи все того же автомата состояний.
На рисунке ниже общее количество тактов, необходимое схеме для достижения результата.
Такое количество определяет задержку получения результата и такой термин, как латентность. Среди этих действий есть как чтение элементов массива из памяти, так и запись результата в выходной массив, расположенный в другом модуле памяти. Если обычный процессор для достижения результата должен будет выполнить массу операций, то такая довольно простая схема справится за 10 тактов. Это уже не так много, но если требуется исключительная производительность, то можно пожертвовать чуть большим количеством ресурсов.
Конвейерное вычисление.
При обычном подходе к реализации тела цикла мы получаем долгое время ожидания результата. При применении конвейерного способа вычислений одна часть схемы занимается одной операцией и передаёт результат на вторую часть, где происходит вторая операция.
После второй операции результат подаётся далее. Независимая параллельная работа таких частей приводит к тому, что в один и тот же момент выполняется несколько независимых операций. Так, в этом примере происходит одновременно считывание последнего числа из входного массива, вычисление с использованием среднего числа из массива и запись результата вычисления после операции над самым первым числом из массива. Как можно заметить, латентность функции сократилась в два раза. Конечно, при этом неизбежно подрастает количество используемых ресурсов.
Использование директив синтеза.
Одним из самых загадочных вопросов во всём этом является способ управления латентностью и количеством используемых в вычислениях ресурсов. Как можно понять, языки Си и С++ не имеют штатных лексических конструкций для использования в той области, где их никогда не ждали. Но по счастью существуют такое понятие как директивы и уж они и являются "заклинаниями", при помощи которых можно контролировать нужный уровень производительности.
В этом примере функция обрабатывает буфер данных, предназначенных для вывода на экран. При размере изображения 640 на 480 пикселей необходимо обработать более трёхсот тысяч чисел, каждое из которых отвечает за цвет своего пикселя на экране. И если ещё для обработки одного пикселя требуется много-шаговый цикл, то очень даже целесообразно распараллелить выполнение тела небольшого цикла чтобы ускорить обработку буфера данных. Делается это при помощи директивы pragma HLS PIPELINE II=1. Таких директив всех разновидностей довольно большое количество и каждая для чего-то предназначена.
всё... Ну почти. Ещё видосик:
.
Viktor2312- RIP
- Сообщения : 15492
Дата регистрации : 2012-08-10
Возраст : 45
Откуда : Пятигорск
 .
.
4
Google анонсировала новый язык программирования Logica.

В своём блоге компания написала, что это декларативный язык логического программирования, предназначенный для манипулирования данными и трансляции программ в SQL. Язык уже поддерживает Google BigQuery, PostgreSQL и SQLite.
Колаб и подробный туториал по работе с Logica доступен по ссылке: Ссылка
.

В своём блоге компания написала, что это декларативный язык логического программирования, предназначенный для манипулирования данными и трансляции программ в SQL. Язык уже поддерживает Google BigQuery, PostgreSQL и SQLite.
Колаб и подробный туториал по работе с Logica доступен по ссылке: Ссылка
.
Viktor2312- RIP
- Сообщения : 15492
Дата регистрации : 2012-08-10
Возраст : 45
Откуда : Пятигорск
 .
.
6
Сервис, чтобы попрактиковаться в изучении команд Git.
На сайте LearnGitBranching можно как решать уже готовые задания, так и тестировать случайные команды на простом репозитории в режиме «песочницы»:
https://github.com/pcottle/learnGitBranching
.
На сайте LearnGitBranching можно как решать уже готовые задания, так и тестировать случайные команды на простом репозитории в режиме «песочницы»:
https://github.com/pcottle/learnGitBranching
.
Viktor2312- RIP
- Сообщения : 15492
Дата регистрации : 2012-08-10
Возраст : 45
Откуда : Пятигорск
 .
.
7
Учёные тайно внедрили уязвимости в ядро Linux.
И всё это было частью их свежего исследования.
Учёные из Миннесотского университета решили провести эксперимент. Они начали внедрять в популярные open source проекты уязвимости под видом свежих патчей. Исследователи хотели узнать, насколько вообще велики шансы провернуть подобное.
В том числе их взор упал и на проект ядра Linux. Связано это с его известностью и адаптированностью по всему миру.
Специалистам удалось «внедрить» часть патчей, добавляющих в ядро уязвимости. Но по итогу они были пойманы с поличным мейнтейнерами проекта.
Один из ведущих разработчиков, поддерживающих Linux-ядро, Грег Крох-Хартман даже написал разъярённое письмо исследователям.
Нашему комьюнити не нравится, когда над ним экспериментируют и «тестируют», отправляя известные исправления, которые либо намеренно ничего не делают, либо намеренно вносят ошибки <…> Из-за этого мне теперь придётся забанить все будущие контрибуции из вашего университета и «похоронить» предыдущие, поскольку они явно были поданы недобросовестно с намерением вызвать проблемы.
Отметим, что научная работа, ради которой всё это затевалось, вышла ещё в феврале 2021 года. Согласно ей, количество успешных «инъекций» уязвимостей составляет около 60% от общего числа попыток.
.
Viktor2312- RIP
- Сообщения : 15492
Дата регистрации : 2012-08-10
Возраст : 45
Откуда : Пятигорск
 Похожие темы
Похожие темы» Статьи, заметки, очерки, разное...
» Статьи, заметки, очерки, разное...
» Статьи, заметки, очерки, разное...
» Статьи, заметки, очерки, разное...
» Статьи, заметки, очерки, разное...
» Статьи, заметки, очерки, разное...
» Статьи, заметки, очерки, разное...
» Статьи, заметки, очерки, разное...
» Статьи, заметки, очерки, разное...
Страница 1 из 1
Права доступа к этому форуму:
Вы не можете отвечать на сообщения