HM-SHA256-FPGA_v001. Теория, статьи, разное...

____Алгоритм использует следующие битовые операции:

ǁ — конкатенация,

+ — сложение,

and — побитовое «И»,

xor — исключающее «ИЛИ»,

shr (shift right) — логический сдвиг вправо,

rotr (rotate right) — циклический сдвиг вправо.

Пояснения:
Все переменные беззнаковые, имеют размер 32 бита и при вычислениях суммируются по модулю 2³²
message — исходное двоичное сообщение
m — преобразованное сообщение

Инициализация переменных
(первые 32 бита дробных частей квадратных корней первых восьми простых чисел [от 2 до 19]):

h0 := 0x6A09E667
h1 := 0xBB67AE85
h2 := 0x3C6EF372
h3 := 0xA54FF53A
h4 := 0x510E527F
h5 := 0x9B05688C
h6 := 0x1F83D9AB
h7 := 0x5BE0CD19

Таблица констант
(первые 32 бита дробных частей кубических корней первых 64 простых чисел [от 2 до 311]):

k[0..63] :=
0x428A2F98, 0x71374491, 0xB5C0FBCF, 0xE9B5DBA5,
0x3956C25B, 0x59F111F1, 0x923F82A4, 0xAB1C5ED5,
0xD807AA98, 0x12835B01, 0x243185BE, 0x550C7DC3,
0x72BE5D74, 0x80DEB1FE, 0x9BDC06A7, 0xC19BF174,
0xE49B69C1, 0xEFBE4786, 0x0FC19DC6, 0x240CA1CC,
0x2DE92C6F, 0x4A7484AA, 0x5CB0A9DC, 0x76F988DA,
0x983E5152, 0xA831C66D, 0xB00327C8, 0xBF597FC7,
0xC6E00BF3, 0xD5A79147, 0x06CA6351, 0x14292967,
0x27B70A85, 0x2E1B2138, 0x4D2C6DFC, 0x53380D13,
0x650A7354, 0x766A0ABB, 0x81C2C92E, 0x92722C85,
0xA2BFE8A1, 0xA81A664B, 0xC24B8B70, 0xC76C51A3,
0xD192E819, 0xD6990624, 0xF40E3585, 0x106AA070,
0x19A4C116, 0x1E376C08, 0x2748774C, 0x34B0BCB5,
0x391C0CB3, 0x4ED8AA4A, 0x5B9CCA4F, 0x682E6FF3,
0x748F82EE, 0x78A5636F, 0x84C87814, 0x8CC70208,
0x90BEFFFA, 0xA4506CEB, 0xBEF9A3F7, 0xC67178F2

Предварительная обработка:

m := message ǁ [единичный бит]
m := m ǁ [k нулевых бит],

где k — наименьшее неотрицательное число, такое что
(L + 1 + K) mod 512 = 448, где L — число бит в сообщении (сравнима по модулю 512 c 448)

m := m ǁ Длина(message)

- длина исходного сообщения в битах в виде 64-битного числа с порядком байтов от старшего к младшему

Далее сообщение обрабатывается последовательными порциями по 512 бит:
разбить сообщение на куски по 512 бит
для каждого куска разбить кусок на 16 слов длиной 32 бита (с порядком байтов от старшего к младшему внутри слова): w[0..15]

Сгенерировать дополнительные 48 слов:

для i от 16 до 63
s0 := (w[i-15] rotr 7) xor (w[i-15] rotr 18) xor (w[i-15] shr 3)
s1 := (w[i-2] rotr 17) xor (w[i-2] rotr 19) xor (w[i-2] shr 10)
w[i] := w[i-16] + s0 + w[i-7] + s1

Инициализация вспомогательных переменных:

a := h0
b := h1
c := h2
d := h3
e := h4
f := h5
g := h6
h := h7

Основной цикл:

для i от 0 до 63
Σ0 := (a rotr 2) xor (a rotr 13) xor (a rotr 22)
Ma := (a and b) xor (a and c) xor (b and c)
t2 := Σ0 + Ma
Σ1 := (e rotr 6) xor (e rotr 11) xor (e rotr 25)
Ch := (e and f) xor ((not e) and g)
t1 := h + Σ1 + Ch + k[i] + w[i]

h := g
g := f
f := e
e := d + t1
d := c
c := b
b := a
a := t1 + t2

Добавить полученные значения к ранее вычисленному результату:

h0 := h0 + a
h1 := h1 + b
h2 := h2 + c
h3 := h3 + d
h4 := h4 + e
h5 := h5 + f
h6 := h6 + g
h7 := h7 + h

Получить итоговое значение хеша:

digest = hash = h0 ǁ h1 ǁ h2 ǁ h3 ǁ h4 ǁ h5 ǁ h6 ǁ h7



___________________________________________________________________________________________

Ch := (e and f) xor ((not e) and g) преобразуем Ch := g xor (e and (f xor g))

Ma := (a and b) xor (a and c) xor (b and c) преобразуем Ma := (a and b) or (c and (a or b))



.

Для общего понимания, что происходит, на примере «hello world». При реализации в Soft, при реализации в "железе", всё так же за исключением некоторых действий.


SHA-256 «hello world». Шаг 1. Предварительная обработка.

1. Преобразуем «hello world» в двоичный вид:

01101000 01100101 01101100 01101100 01101111 00100000 01110111 01101111
01110010 01101100 01100100

2. Добавим одну единицу:

01101000 01100101 01101100 01101100 01101111 00100000 01110111 01101111
01110010 01101100 01100100 1

3. Заполняем нулями до тех пор, пока данные не станут кратны 512 без последних 64 бит (в нашем случае 448 бит):

01101000 01100101 01101100 01101100 01101111 00100000 01110111 01101111
01110010 01101100 01100100 10000000 00000000 00000000 00000000 00000000
00000000 00000000 00000000 00000000 00000000 00000000 00000000 00000000
00000000 00000000 00000000 00000000 00000000 00000000 00000000 00000000
00000000 00000000 00000000 00000000 00000000 00000000 00000000 00000000
00000000 00000000 00000000 00000000 00000000 00000000 00000000 00000000
00000000 00000000 00000000 00000000 00000000 00000000 00000000 00000000

4. Добавим 64 бита в конец, где 64 бита — целое число с порядком байтов big-endian, обозначающее длину входных данных в двоичном виде. В нашем случае 88, в двоичном виде — «1011000».

01101000 01100101 01101100 01101100 01101111 00100000 01110111 01101111
01110010 01101100 01100100 10000000 00000000 00000000 00000000 00000000
00000000 00000000 00000000 00000000 00000000 00000000 00000000 00000000
00000000 00000000 00000000 00000000 00000000 00000000 00000000 00000000
00000000 00000000 00000000 00000000 00000000 00000000 00000000 00000000
00000000 00000000 00000000 00000000 00000000 00000000 00000000 00000000
00000000 00000000 00000000 00000000 00000000 00000000 00000000 00000000
00000000 00000000 00000000 00000000 00000000 00000000 00000000 01011000

Теперь у нас есть ввод, который всегда будет без остатка делиться на 512.


Шаг 2. Инициализация значений хеша (h).

Создадим 8 значений хеша. Это константы, представляющие первые 32 бита дробных частей квадратных корней первых 8 простых чисел: 2, 3, 5, 7, 11, 13, 17, 19.

h0 := 0x6a09e667
h1 := 0xbb67ae85
h2 := 0x3c6ef372
h3 := 0xa54ff53a
h4 := 0x510e527f
h5 := 0x9b05688c
h6 := 0x1f83d9ab
h7 := 0x5be0cd19

Шаг 3. Инициализация округлённых констант (k).

0x428a2f98 0x71374491 0xb5c0fbcf 0xe9b5dba5 0x3956c25b 0x59f111f1 0x923f82a4 0xab1c5ed5
0xd807aa98 0x12835b01 0x243185be 0x550c7dc3 0x72be5d74 0x80deb1fe 0x9bdc06a7 0xc19bf174
0xe49b69c1 0xefbe4786 0x0fc19dc6 0x240ca1cc 0x2de92c6f 0x4a7484aa 0x5cb0a9dc 0x76f988da
0x983e5152 0xa831c66d 0xb00327c8 0xbf597fc7 0xc6e00bf3 0xd5a79147 0x06ca6351 0x14292967
0x27b70a85 0x2e1b2138 0x4d2c6dfc 0x53380d13 0x650a7354 0x766a0abb 0x81c2c92e 0x92722c85
0xa2bfe8a1 0xa81a664b 0xc24b8b70 0xc76c51a3 0xd192e819 0xd6990624 0xf40e3585 0x106aa070
0x19a4c116 0x1e376c08 0x2748774c 0x34b0bcb5 0x391c0cb3 0x4ed8aa4a 0x5b9cca4f 0x682e6ff3
0x748f82ee 0x78a5636f 0x84c87814 0x8cc70208 0x90befffa 0xa4506ceb 0xbef9a3f7 0xc67178f2

Шаг 4. Основной цикл.

Следующие шаги будут выполняться для каждого 512-битного «куска» входных данных. Наша тестовая фраза «hello world» довольно короткая, поэтому «кусок» всего один. На каждой итерации цикла мы будем изменять значения хеш-функций h0–h7, чтобы получить окончательный результат.


Шаг 5. Создаём очередь сообщений (w).

1. Копируем входные данные из шага 1 в новый массив, где каждая запись является 32-битным словом:

01101000011001010110110001101100 01101111001000000111011101101111
01110010011011000110010010000000 00000000000000000000000000000000
00000000000000000000000000000000 00000000000000000000000000000000
00000000000000000000000000000000 00000000000000000000000000000000
00000000000000000000000000000000 00000000000000000000000000000000
00000000000000000000000000000000 00000000000000000000000000000000
00000000000000000000000000000000 00000000000000000000000000000000
00000000000000000000000000000000 00000000000000000000000001011000

2. Добавляем ещё 48 слов, инициализированных нулями, чтобы получить массив w[0…63]:

01101000011001010110110001101100 01101111001000000111011101101111
01110010011011000110010010000000 00000000000000000000000000000000
00000000000000000000000000000000 00000000000000000000000000000000
00000000000000000000000000000000 00000000000000000000000000000000
00000000000000000000000000000000 00000000000000000000000000000000
00000000000000000000000000000000 00000000000000000000000000000000
00000000000000000000000000000000 00000000000000000000000000000000
00000000000000000000000000000000 00000000000000000000000001011000
00000000000000000000000000000000 00000000000000000000000000000000
00000000000000000000000000000000 00000000000000000000000000000000
00000000000000000000000000000000 00000000000000000000000000000000
00000000000000000000000000000000 00000000000000000000000000000000
...
...
00000000000000000000000000000000 00000000000000000000000000000000

3. Изменяем нулевые индексы в конце массива, используя следующий алгоритм:

• For i from w[16…63]:
  
  
  
  • s0 = (w[i-15] rightrotate 7) xor (w[i-15] rightrotate 18) xor (w[i-15] righthift 3)
    
    
  • s1 = (w[i-2] rightrotate 17) xor (w[i-2] rightrotate 19) xor (w[i-2] righthift 10)
    
    
  • w [i] = w[i-16] + s0 + w[i-7] + s1
    
  
  
  

Давайте посмотрим, как это работает для w[16]:

w[1] rightrotate 7:
 01101111001000000111011101101111 -> 11011110110111100100000011101110
w[1] rightrotate 18:
 01101111001000000111011101101111 -> 00011101110110111101101111001000
w[1] rightshift 3:
 01101111001000000111011101101111 -> 00001101111001000000111011101101

s0 = 11011110110111100100000011101110 XOR 00011101110110111101101111001000 XOR 00001101111001000000111011101101

s0 = 11001110111000011001010111001011

w[14] rightrotate 17:
 00000000000000000000000000000000 -> 00000000000000000000000000000000
w[14] rightrotate19:
 00000000000000000000000000000000 -> 00000000000000000000000000000000
w[14] rightshift 10:
 00000000000000000000000000000000 -> 00000000000000000000000000000000

s1 = 00000000000000000000000000000000 XOR 00000000000000000000000000000000 XOR 00000000000000000000000000000000

s1 = 00000000000000000000000000000000

w[16] = w[0] + s0 + w[9] + s1

w[16] = 01101000011001010110110001101100 + 11001110111000011001010111001011 + 00000000000000000000000000000000 + 00000000000000000000000000000000

// сложение рассчитывается по модулю 2^32

w[16] = 00110111010001110000001000110111

Это оставляет нам 64 слова в нашей очереди сообщений (w):

01101000011001010110110001101100 01101111001000000111011101101111
01110010011011000110010010000000 00000000000000000000000000000000
00000000000000000000000000000000 00000000000000000000000000000000
00000000000000000000000000000000 00000000000000000000000000000000
00000000000000000000000000000000 00000000000000000000000000000000
00000000000000000000000000000000 00000000000000000000000000000000
00000000000000000000000000000000 00000000000000000000000000000000
00000000000000000000000000000000 00000000000000000000000001011000
00110111010001110000001000110111 10000110110100001100000000110001
11010011101111010001000100001011 01111000001111110100011110000010
00101010100100000111110011101101 01001011001011110111110011001001
00110001111000011001010001011101 10001001001101100100100101100100
01111111011110100000011011011010 11000001011110011010100100111010
10111011111010001111011001010101 00001100000110101110001111100110
10110000111111100000110101111101 01011111011011100101010110010011
00000000100010011001101101010010 00000111111100011100101010010100
00111011010111111110010111010110 01101000011001010110001011100110
11001000010011100000101010011110 00000110101011111001101100100101
10010010111011110110010011010111 01100011111110010101111001011010
11100011000101100110011111010111 10000100001110111101111000010110
11101110111011001010100001011011 10100000010011111111001000100001
11111001000110001010110110111000 00010100101010001001001000011001
00010000100001000101001100011101 01100000100100111110000011001101
10000011000000110101111111101001 11010101101011100111100100111000
00111001001111110000010110101101 11111011010010110001101111101111
11101011011101011111111100101001 01101010001101101001010100110100
00100010111111001001110011011000 10101001011101000000110100101011
01100000110011110011100010000101 11000100101011001001100000111010
00010001010000101111110110101101 10110000101100000001110111011001
10011000111100001100001101101111 01110010000101111011100000011110
10100010110101000110011110011010 00000001000011111001100101111011
11111100000101110100111100001010 11000010110000101110101100010110

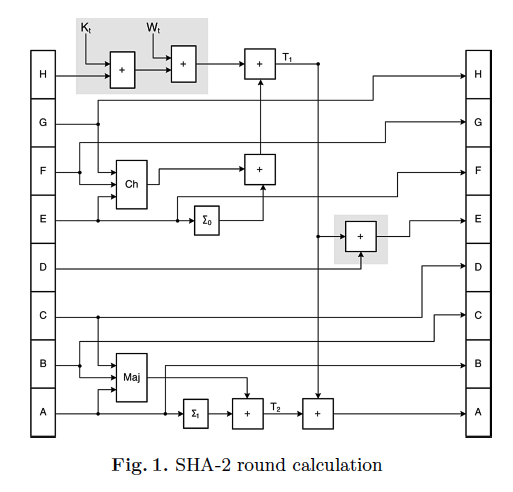
Шаг 6. Цикл сжатия.

1. Инициализируем переменные a, b, c, d, e, f, g, h и установим их равными текущим значениям хеша соответственно. h0, h1, h2, h3, h4, h5, h6, h7.

2. Запустим цикл сжатия, который будет изменять значения a…h . Цикл выглядит следующим образом:

• for i from 0 to 63
  
  
  
  • S1 = (e rightrotate 6) xor (e rightrotate 11) xor (e rightrotate 25)
    
    
  • ch = (e and f) xor ((not e) and g)
    
    
  • temp1 = h + S1 + ch + k[i] + w[i]
    
    
  • S0 = (a rightrotate 2) xor (a rightrotate 13) xor (a rightrotate 22)
    
    
  • maj = (a and b) xor (a and c) xor (b and c)
    
    
  • temp2 := S0 + maj
    
    
  • h = g
    
    
  • g = f
    
    
  • f = e
    
    
  • e = d + temp1
    
    
  • d = c
    
    
  • c = b
    
    
  • b = a
    
    
  • temp1 + temp2
    
  
  
  

Давайте пройдём первую итерацию. Сложение рассчитывается по модулю 2^32:

a = 0x6a09e667 = 01101010000010011110011001100111
b = 0xbb67ae85 = 10111011011001111010111010000101
c = 0x3c6ef372 = 00111100011011101111001101110010
d = 0xa54ff53a = 10100101010011111111010100111010
e = 0x510e527f = 01010001000011100101001001111111
f = 0x9b05688c = 10011011000001010110100010001100
g = 0x1f83d9ab = 00011111100000111101100110101011
h = 0x5be0cd19 = 01011011111000001100110100011001

e rightrotate 6:
 01010001000011100101001001111111 -> 11111101010001000011100101001001
e rightrotate 11:
 01010001000011100101001001111111 -> 01001111111010100010000111001010
e rightrotate 25:
 01010001000011100101001001111111 -> 10000111001010010011111110101000
S1 = 11111101010001000011100101001001 XOR 01001111111010100010000111001010 XOR 10000111001010010011111110101000
S1 = 00110101100001110010011100101011

e and f:
   01010001000011100101001001111111
 & 10011011000001010110100010001100 =
   00010001000001000100000000001100
not e:
 01010001000011100101001001111111 -> 10101110111100011010110110000000
(not e) and g:
   10101110111100011010110110000000
 & 00011111100000111101100110101011 =
   00001110100000011000100110000000
ch = (e and f) xor ((not e) and g)
  = 00010001000001000100000000001100 xor 00001110100000011000100110000000
  = 00011111100001011100100110001100

// k[i] is the round constant
// w[i] is the batch
temp1 = h + S1 + ch + k[i] + w[i]
temp1 = 01011011111000001100110100011001 + 00110101100001110010011100101011 + 00011111100001011100100110001100 + 1000010100010100010111110011000 + 01101000011001010110110001101100
temp1 = 01011011110111010101100111010100

a rightrotate 2:
 01101010000010011110011001100111 -> 11011010100000100111100110011001
a rightrotate 13:
 01101010000010011110011001100111 -> 00110011001110110101000001001111
a rightrotate 22:
 01101010000010011110011001100111 -> 00100111100110011001110110101000
S0 = 11011010100000100111100110011001 XOR 00110011001110110101000001001111 XOR 00100111100110011001110110101000
S0 = 11001110001000001011010001111110

a and b:
   01101010000010011110011001100111
 & 10111011011001111010111010000101 =
   00101010000000011010011000000101
a and c:
   01101010000010011110011001100111
 & 00111100011011101111001101110010 =
   00101000000010001110001001100010
b and c:
   10111011011001111010111010000101
 & 00111100011011101111001101110010 =
   00111000011001101010001000000000
maj = (a and b) xor (a and c) xor (b and c)
   = 00101010000000011010011000000101 xor 00101000000010001110001001100010 xor 00111000011001101010001000000000
   = 00111010011011111110011001100111

temp2 = S0 + maj
     = 11001110001000001011010001111110 + 00111010011011111110011001100111
     = 00001000100100001001101011100101

h = 00011111100000111101100110101011
g = 10011011000001010110100010001100
f = 01010001000011100101001001111111
e = 10100101010011111111010100111010 + 01011011110111010101100111010100
 = 00000001001011010100111100001110
d = 00111100011011101111001101110010
c = 10111011011001111010111010000101
b = 01101010000010011110011001100111
a = 01011011110111010101100111010100 + 00001000100100001001101011100101
 = 01100100011011011111010010111001

Все расчёты выполняются ещё 63 раза, изменяя переменные а…h. В итоге мы должны получить следующее:

h0 = 6A09E667 = 01101010000010011110011001100111
h1 = BB67AE85 = 10111011011001111010111010000101
h2 = 3C6EF372 = 00111100011011101111001101110010
h3 = A54FF53A = 10100101010011111111010100111010
h4 = 510E527F = 01010001000011100101001001111111
h5 = 9B05688C = 10011011000001010110100010001100
h6 = 1F83D9AB = 00011111100000111101100110101011
h7 = 5BE0CD19 = 01011011111000001100110100011001

a = 4F434152 = 001001111010000110100000101010010
b = D7E58F83 = 011010111111001011000111110000011
c = 68BF5F65 = 001101000101111110101111101100101
d = 352DB6C0 = 000110101001011011011011011000000
e = 73769D64 = 001110011011101101001110101100100
f = DF4E1862 = 011011111010011100001100001100010
g = 71051E01 = 001110001000001010001111000000001
h = 870F00D0 = 010000111000011110000000011010000

Шаг 7. Изменяем окончательные значения.

После цикла сжатия, но ещё внутри основного цикла, мы модифицируем значения хеша, добавляя к ним соответствующие переменные a…h. Как обычно, всё сложение происходит по модулю 2^32.

h0 = h0 + a = 10111001010011010010011110111001
h1 = h1 + b = 10010011010011010011111000001000
h2 = h2 + c = 10100101001011100101001011010111
h3 = h3 + d = 11011010011111011010101111111010
h4 = h4 + e = 11000100100001001110111111100011
h5 = h5 + f = 01111010010100111000000011101110
h6 = h6 + g = 10010000100010001111011110101100
h7 = h7 + h = 11100010111011111100110111101001

Шаг 8. Получаем финальный хеш.

digest = h0 append h1 append h2 append h3 append h4 append h5 append h6 append h7
      = B94D27B9934D3E08A52E52D7DA7DABFAC484EFE37A5380EE9088F7ACE2EFCDE9

«How SHA-2 Works Step-By-Step (SHA-256)»



.