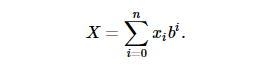Модулярная арифметика.

Пост для важного.


Система остаточных классов (Не долго мучалась старушка, в высоковольтных проводах, и осталась от неё, лишь обгоревшая тушка. Ссылка померла, а жаль, но не фатально...)

Скачать (Модулярная арифметика .pdf)

Читать (Mod и остаток — не одно и то же)

Червяков Н. И., Велигоша А. В., Калмыков И. А., Иванов П. Е. Цифровые фильтры в системе остаточных классов // Радиоэлектроника. — 1995. Т. 38, № 8. — С. 11–20. Червяков Н. И., Евдокимов А. А., Головко А. Н. Гибридная нейронная сеть для коррекции ошибок «на лету» в системе остаточных классов // Нейрокомпьютеры: разработка, применение. — 2009, № 10. — С. 13–20.

Ляхов, П. А. Сравнительный анализ методов перевода чисел из системы остаточных классов в позиционную систему счисления / П. А. Ляхов, Ю. В. Голошубова, Е. А. Попова. — Текст : непосредственный // Молодой ученый. — 2017. — № 22 (156). — С. 1-6.
















.

Ни для кого не секрет, что математика – наука абстрактная и в своём "чистом" виде никакого отношения к реальному миру не имеет. Многие, конечно попробуют эту мысль оспорить. Однако заставляет задуматься хотя бы тот факт, что разные народы в различные периоды времени даже считали по-разному. Стоит только вспомнить крайне неэффективную систему счисления древних римлян. Греки вместо чисел использовали буквы собственного алфавита, как и славяне. В Вавилоне появилась шестидесятеричная система счисления, которая нашла отражение в подсчёте времени (60 минут в часе, 60 секунд в минуте) и углов. И египтяне конечно же отличились, первыми придумав десятичную, хотя и непозиционную, систему счисления. Иными словами – кто как придумал, тот так и считал.

Настоящую революцию произвела придуманная в Индии не позднее V века позиционная десятичная система счисления. Основным достижением индийцев стало использование в качестве одной из цифр нуля. Именно этот факт делает данную систему счисления столь удобной – теперь можно записать любое число, используя всего 10 различных символов и не изобретая новый для каждого нового разряда. Величина числа зависит от позиции в нём цифр и их количества.

Изобретение современной позиционной системы счисления (арабских цифр) дало серьёзный импульс развитию математики. Была фактически решена проблема арифметических операций – их теперь можно было выполнять интуитивно понятным, быстрым и эффективным способом, который не меняется уже более пятнадцати веков. Дальнейшее развитие идеи позиционности сделало принципиально возможным создание современной вычислительной техники – она функционирует на основе двоичной системы счисления.



Однако, как показал опыт последних десятилетий, в некоторых случаях именно позиционный подход к записи чисел вызывает определенные неудобства. Основная проблема заключена в обработке чисел – раз от позиции цифры зависит величина числа, то в процессе расчётов из-за переносов они должны обрабатываться последовательно, от младшего к старшему. Очевидный вывод, знакомо с детства: сначала складываем единицы, затем десятки, сотни, тысячи...  На первый взгляд ничего страшного в такой привычной картине нет. Но стоит обратить внимание на возможности вычислительной техники.

Современные вычислительные системы, несмотря на всю свою мощь, всё-таки ограничены. И дело даже не в том, что они не могут, например, сделать точный прогноз погоды или расшифровать ДНК. Ограниченность проявляется в самой незначительной, казалось бы, части – диапазоне работы с числами. Просто компьютер способен работать лишь с ограниченным отрезком чисел, который определяется разрядной сеткой процессора. Многие устройства "понимают" числа размером 32 бита (двоичных разряда), другие – 64. Крайне мало 128-ми битных вычислительных элементов, всё остальное – вообще единичные случаи. Малая разрядность чисел приводит к невысокой точности вычислений, а многие алгоритмы и вовсе требуют запредельной разрядности. Так например схема шифрования RSA в современном варианте считается достаточно безопасной при длине ключа 2048 бит, что вызывает определенные затруднения при реализации.

Первую проблему, возникающая перед разработчиком в данной ситуации, можно сформулировать следующим образом: как производить вычисления с числами большой разрядности, если архитектура вычислительных систем их просто не поддерживает? Но при ближайшем рассмотрении данный вопрос даже не является проблемой. Ответ на него скрыт в самой идее позиционных систем счисления.

Назовем некоторое число b основанием системы счисления. Тогда число X, представленное в системе счисления с основанием b набором из n цифр {x₀,x₁,...,x_n}, определяется следующим образом:


Например, в десятичной системе счисления число 5318 есть ни что иное, как 5 ⋅ 10³ + 3 ⋅ 10² + 1 ⋅ 10¹ + 8 ⋅ 10⁰. Таким же образом всё работает в двоичной, троичной, восьмеричной системе и так далее. А теперь представим, что основанием системы счисления является число 2³². Все числа от 0 до 2³² − 1 = 4294967295 будут условными цифрами данной системы. Причём данный диапазон полностью покрывает все 32-х битные числа. То есть теперь любое число можно представить в виде набора тридцатидвухбитных цифр. Такой подход применяется для организации вычислений с большими числами на стандартной аппаратуре. При этом мы всё равно не избавляемся от сложностей: нельзя забывать о необходимости выполнять переносы между разрядами нашего большого числа, возникающие при выполнении операций сложение и умножение, что делает вычисления достаточно медленными. Некоторый выход из ситуации предлагает модулярная арифметика.



Ранее мы пришли к выводу, что позиционность не всегда хорошо. Рассмотрим теперь непозиционный подход к системам счисления. Под непозиционностью понимается отсутствие очевидной связи между разрядами или, иными словами, отсутствие переносов. Одной из самых используемых непозиционных систем счисления является Система остаточных классов (СОК, Residue Number System – RNS). СОК основывается на теории сравнений и была предложена советским математиком Израилем Яковлевичем Акушским в 50-е годы двадцатого века. Теорию вычислений в СОК иногда называют модулярной арифметикой, основной теоремой которой является Китайская теорема об остатках (КТО, Chinese remainder theorem – CRT), одна из формулировок которой приведена ниже.


Последовательность (x₁,x₂,...,x_n) и есть представление числа X в системе остаточных классов. Каждое из чисел x_i называется разрядом числа в СОК. Отметим, что числа x_i являются остатками от деления на числа p_i, откуда 0⩽x_i<p_i. Именно этот факт отражает основные свойства СОК – снижение разрядности. Всё дело в том, что для вычисления суммы или произведения двух чисел, представленных в СОК, достаточно сложить и умножить соответственные остатки-разряды:


Преимущества такого подхода очевидны: мы выполняем операции одновременно по различным основаниям так как они не зависят друг от друга. Иными словами, помимо снижения разрядности мы добавляем параллелизм, который принципиально невозможен в позиционной системе. Это идеально ложится под современные вычислительные средства: параллельные вычисления развиваются в последнее время максимально возможными темпами, проявляясь не только в архитектуре компьютеров, но и при разработке встраиваемых решений, основанных, например, на микросхемах ПЛИС архитектуры FPGA.

Проведенные исследования показывают, что во многих задачах использование СОК совместно с параллельными вычислениями приводит к значительному увеличению производительности. Например, операция возведения в степень в СОК для больших чисел может быть реализована крайне эффективно, что приведёт к сверхлинейному ускорению, что отражено в графике на рисунке 1.


Основной проблемой модулярной арифметики и СОК в частности является существование так называемых немодульных операций. К такому классу операций относятся, например, сравнение и деление чисел. Данные операции имеют позиционную природу и не могут быть выполнены без вычисления какой-либо характеристики числа, определяющей его позицию в числовом ряде, что приводит к восстановлению позиционного представления числа в том или ином роде. Работы многих исследователей направлены на максимальную оптимизацию немодульных операций в СОК. Однако наиболее эффективными остаются алгоритмы, сводящие использование таких операций к минимуму. Хорошей областью для применения СОК таким образом является криптография, сводящаяся к умножению, сложению и возведению в степень.



Рассмотрим работу в СОК с основаниями {2, 3, 5, 7}. Динамическим диапазоном для данной системы будет число P = 2 ⋅ 3 ⋅ 5 ⋅ 7 = 210, следовательно, в соответствии с КТО все числа, представимые в ней, не должны превышать этого числа. Переведём числа 63 и 79 в нашу СОК, для этого возьмём остатки от деления данных чисел по каждому из модулей и составим из них кортежи:

63 = (1, 0, 3, 0), 79 = (1, 1, 4, 2)

Найдем сумму данных чисел:

63 + 79= (1 + 1 mod 2, 0 + 1 mod 3, 3 + 4 mod 5, 0 + 2 mod 7) = (0, 1, 2, 2).

Для проверки результата найдём позиционное значение суммы и так же переведём его в СОК.

63 + 79 = 142 = (0, 1, 2, 2).

Умножим полученное число на 2 в СОК. Здесь 2 = (0, 2, 2, 2)

142 ⋅ 2 = (0, 1, 2, 2) ⋅ (0, 2, 2, 2) = (0, 2, 4, 4),

что соответствует реальности, так как 142 ⋅ 2 = 284 mod 210 = 74 = (0, 2, 4, 4).


Несмотря на все свои преимущества, СОК, как было отмечено ранее, не может быть панацеей от всех бед в длинной арифметике, однако конкретные проблемно-ориентированные задачи в ней реализуются крайне эффективно. Наибольший положительный эффект СОК уже сыграла в следующих направлениях, помимо уже описанного:

• СОК позволяет упростить и уменьшить архитектуру вычислительных электронных устройств, за счёт чего повышается не только скорость, но и энергетическая эффективность продуктов.
  
  
• СОК часто используется как средство для синтеза устройств высокой надёжности, её "параллельная" природа позволяет за счёт введения избыточных оснований строить высокоэффективные помехоустойчивые коды.
  
  
• Криптографические приложения не ограничиваются одним лишь ускорением работы с длинными числами; СОК является хорошей базой для построения схем разделения секрета, обладающих выгодными относительно аналогов свойствами.
  
  
• В системах цифровой обработки сигналов (ЦОС, DSP) СОК показала себя как выгодный инструмент повышения эффективности цифровых фильтров, о чём свидетельствует огромное количество работ в данной области.
  
  
• Некоторые приложения нашла СОК в системах связи, примером чему является оптимизация технологии CDMA за счёт внедрения модулярных преобразований.
  

Все преимущества, возникающие при применении СОК, получены благодаря тому, что мы изменили свой взгляд на системы счисления. Иногда нетривиальный взгляд на математические объекты может дать перспективные результаты.

1. Червяков Н. И., Сахнюк П. А., Шапошников А. В., Макоха А. Н. Нейрокомпьютеры в остаточных классах. – М.: Радиотехника, 2003. – 272 с.
   
   
2. Дерябин М.А., Зайцев А.А. Использование модулярной арифметики для ускорения выполнения операций с числами большой разрядности. // Вестник УГАТУ – Уфа: Издательство УГАТУ, 2013. Т. 17, № 5 (58). – С. 245–251.
   
   
3. Червяков Н. И., Евдокимов А. А., Галушкин А. И., Лавриненко И. Н., Лавриненко А. В. Применение искусственных нейронных сетей и системы остаточных классов в криптографии. – М.: «Физматлит», 2012. – 280 с.
   

.

* резерв...
















...

Обычный компьютер способен работать лишь с ограниченным отрезком чисел, который определяется разрядной сеткой процессора. Самые простые процессоры, подобные тем, что входят в состав микроконтроллеров для управления бытовой техникой, «понимают» числа размером в 8 двоичных разрядов (битов), более «продвинутые» — 32 бита, в последнее время распространены персональные компьютеры с разрядностью 64 бита. Казалось бы, в 64 двоичных разряда (около двадцати десятичных разрядов) укладывается любое потребное для практических нужд число. Однако многие совсем не редко встречающиеся алгоритмы требуют куда большей разрядности.

Простой пример представляют популярные схемы шифрования: так, алгоритм RSA, который, например, используется в распространенном интернет-протоколе SSL, в наше время считается достаточно безопасным при длине ключа 2048 бит, что вызывает определенные затруднения при реализации его на 32- и 64-битных машинах. В современных двоичных машинах такая проблема решается переходом к кратным системам счисления (например, с основанием 2¹⁶ или 2³²), однако получающиеся алгоритмы оказываются весьма громоздкими — при каждом удвоении размера RSA-ключа время, затрачиваемое на дешифровку, увеличивается в 6–7 раз.

Еще в 1950-е годы было предложено решение для работы с большими числами, основанное на одной из разновидностей непозиционных систем счисления — системе остаточных классов (СОК — Residue Number System, RNS), иначе называемой модулярной арифметикой. Это решение оказалось универсальным для многих применений и широко используется по сей день в составе многих алгоритмов. Далее рассказывается о том, как в СССР были спроектированы высоконадёжные специализированные машины на основе СОК, находившиеся в эксплуатации до самого последнего времени.

Система остаточных классов (СОК) основана на так называемой китайской теореме об остатках:

Пусть p₁, p₂, ..., p_n есть некоторые натуральные взаимно простые числа и P = p₁ × p₂ × ... × p_n. Тогда любое число X, такое что 0 ≤ X < P может быть однозначно представлено в виде последовательности (x₁, x₂, ..., x_n), где x_i = X mod p_i.

Последовательность (x₁, x₂, ..., x_n) и есть представление числа X в системе остаточных классов. Каждое из чисел x_i называется разрядом числа в СОК. Отметим, что числа x_i являются остатками от деления на числа pi (операция mod — это и есть операция нахождения остатка), откуда 0 ≤ x_i < p_i. Именно этот факт отражает основные свойства СОК — снижение разрядности. Более подробно этот вопрос рассмотрен, например, в заметке математика Максима Дерябина

Дерябин М. Система остаточных классов // Научный блог Максима Дерябина.

http://mderyabin.ru/rns/

Для вычисления суммы (или произведения) двух чисел, представленных в СОК, достаточно сложить (или перемножить) соответственные остатки-разряды. Так как система непозиционная, это можно делать совершенно независимо друг от друга для каждого разряда, операции переноса в следующий разряд здесь не требуются. Малая разрядность остатков обеспечивает возможность реализации табличной арифметики, при которой вместо вычисления результата операции каждый раз в память машины заранее помещается таблица готовых значений. Операция в СОК при такой табличной арифметике и соответствующей конвейеризации выполняется за один машинный такт для сколь угодно большого числа (количество разрядов в котором зависит лишь от конструкции машины). Это позволяет чрезвычайно эффективно выполнять некоторые распространенные классы задач, сводящихся к сложению, умножению и возведению в степень многоразрядных чисел.

...

Пометки.


*
Для представления 32-х битных чисел достаточно следующей системы модулей:
(7, 11, 13, 17, 19, 23, 29, 31) – все они взаимнопросты друг с другом,
их произведение равно 6685349671 > 4294967296. Каждый из модулей не превышает 5 бит,
то есть операции сложения и умножения будут производиться над 5-битными числами.

*
...






.

Оставлю тут для себя.











.

Разбор полётов, пока я не забыл.

Пример.

Рассмотрим работу в СОК с основаниями {2, 3, 5, 7}. Динамическим диапазоном для данной системы будет число P = 2 ⋅ 3 ⋅ 5 ⋅ 7 = 210, следовательно, в соответствии с КТО все числа, представимые в ней, не должны превышать этого числа. Переведём числа 63 и 79 в нашу СОК, для этого возьмём остатки от деления данных чисел по каждому из модулей и составим из них кортежи:

63 = (1, 0, 3, 0), 79 = (1, 1, 4, 2)

Разгребаем.

63 делим на 2, получаем 31,5. Если 31 умножаем на 2 получаем 62 и 63 минус 62 остаток 1

63 делим на 3, получаем 21. Остаток 0

63 делим на 5, получаем 12,6. Если 12 умножаем на 5 получаем 60 и 63 минус 60 остаток 3

63 делим на 7, получаем 9. Остаток 0

Вот и получили (1, 0, 3, 0)

То же самое делаем с числом 79:

79 делим на 2, получаем 39,5. Если 39 умножаем на 2 получаем 78 и 79 минус 78 остаток 1

79 делим на 3, получаем 26, 333... Если 26 умножаем на 3 получаем 78 и 79 минус 78 остаток 1

79 делим на 5, получаем 15,8. Если 15 умножае на 5 получаем 75 и 79 минус 75 остаток 4

79 делим на 7, получаем 11,285... Если 11 умножаем на 7 получаем 77 и 79 минус 77 остаток 2

Вот и получили (1, 1, 4, 2)

Найдём сумму данных чисел:

63 + 79= (1 + 1 mod 2, 0 + 1 mod 3, 3 + 4 mod 5, 0 + 2 mod 7) = (0, 1, 2, 2).

Тут у нас выходит:

2 mod 2,
1 mod 3,
7 mod 5,
2 mod 7

Это нужно начертить:

Первая цифра, это на сколько шагов нужно переместиться по часовой стрелке. Вторая, после mod сколько делений на шкале.




Для проверки результата найдём позиционное значение суммы и так же переведём его в СОК.

63 + 79 = 142 = (0, 1, 2, 2).

Разгребаем.

142 делим на 2, получаем 71. Остаток 0

142 делим на 3, получаем 47,333... Если 47 умножаем на 3 получаем 141 и 142 минус 141 остаток 1

142 делим на 5, получаем 28,4. Если 28 умножаем на 5 получаем 140 и 142 минус 140 остаток 2

142 делим на 7, получаем 20,285... Если 20 умножаем на 7 получаем 140 и 142 минус 140 остаток 2

Всё верно (0, 1, 2, 2)

Умножим полученное число на 2 в СОК. Здесь 2 = (0, 2, 2, 2)

142 ⋅ 2 = (0, 1, 2, 2) ⋅ (0, 2, 2, 2) = (0, 2, 4, 4),

что соответствует реальности, так как 142 ⋅ 2 = 284 mod 210 = 74 = (0, 2, 4, 4).


Вот забавно выходит, было бы сейчас начало 40-х, то вот пока сидел, ну в нужном месте, целое устройство получилось разработать, у нас, например, 63 mod 2. И вот мы бы взяли ленту, загрузили в протягивающее устройство, а на ленте у нас было бы 63 отверстия небольших, и ползунок, лента протягивается, медленно, не спеша, и как только ползунок совпадает с отверстием, он соединяется с площадкой под лентой, которая под напряжением, на реле поступает напряжение. А у нас двигатель, который постоянно вращается, но с нашим барабаном, имеющим два положение, соединён муфтой, пока реле обесточено, стопор стопорить вторую половину муфты и наш барабан, как только реле сработало, оттянуло стопор, барабан при помощи трения в муфте, прокрутился на один оборот, за один импульс - на одно деление. И так 63 раза, столько раз сколько отверстий, и на 63 разе, контакты на барабане были бы на риске 1, получили результат один

Переставляем ленту на механизм протяжки второго и т. д. О! Параллелизм, четыре девушки, вставляют ленту синхронно в четыре устройства и одновременно запускают, ответ будет готов сразу на четырёх устройствах...
Ха-ха-ха...
А то вот тут 20-е XXI века, и теперь сиди ломай голову, как это сделать, ни реле, ни муфт...