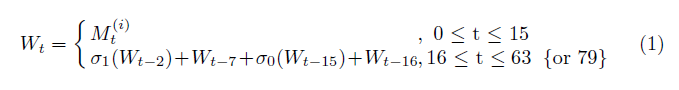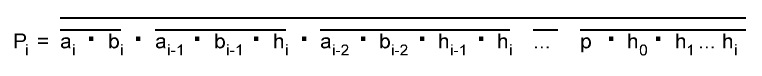Последние темы
» Вити больше нет!автор bug19 Пн Фев 20 2023, 19:54
» Собираем оригинальный Орион 128
автор bug19 Пн Фев 20 2023, 19:47
» Проблема плющеного экрана ОРИОНА
автор kanzler Пн Ноя 28 2022, 12:05
» Орион 128 и его клоны возрождение 2019-2022 год
автор kanzler Пн Ноя 28 2022, 12:03
» Электроника КР-04. Информация, документы, фото.
автор kanzler Пн Ноя 28 2022, 12:02
» Новости форума
автор kanzler Пн Ноя 28 2022, 11:52
» Орион-128 НГМД запуск 2021 года
автор matrixplus Сб Сен 10 2022, 17:36
» ПЗУ F800 для РК86
автор ведущий_специалист Сб Сен 10 2022, 10:37
» Микропроцессорная лаборатория "Микролаб К580ИК80", УМК-80, УМПК-80 и др.
автор Электротехник Вт Июл 26 2022, 19:33
» Орион-128 SD карта в Орионе
автор matrixplus Чт Июн 02 2022, 09:00
» 7 Мая. День Радио!
автор Viktor2312 Чт Май 12 2022, 10:58
» Серия: Массовая радио библиотека. МРБ
автор Viktor2312 Ср Май 11 2022, 12:17
» Полезные книги
автор Viktor2312 Пн Май 09 2022, 15:07
» Орион 128 Стандарты портов и системной шины Х2
автор matrixplus Вс Май 08 2022, 23:08
» Орион-128 и Орион ПРО еще раз про блоки питания
автор matrixplus Вс Май 08 2022, 19:09
» Орион-128 Программаторы
автор matrixplus Вс Май 08 2022, 19:02
» Орион ПРО история сборки 2021 до 2022
автор matrixplus Вс Май 08 2022, 18:47
» Анонсы монет (New coin).
автор Viktor2312 Сб Май 07 2022, 23:11
» Хочу свой усилок для квартиры собрать не спеша
автор Viktor2312 Сб Май 07 2022, 19:33
» Амфитон 25у-002С
автор Viktor2312 Сб Май 07 2022, 09:38
» Майнер: T-Rex
автор Viktor2312 Вс Май 01 2022, 09:12
» GoWin. Изучение документации. SUG100-2.6E_Gowin Software User Guide. Среда разработки EDA.
автор Viktor2312 Пн Апр 25 2022, 01:01
» GoWin. Изучение документации. UG286-1.9.1E Gowin Clock User Guide.
автор Viktor2312 Сб Апр 23 2022, 18:22
» GoWin. Documentation Database. Device. GW2A.
автор Viktor2312 Ср Апр 20 2022, 14:08
» GOWIN AEC IP
автор Viktor2312 Ср Апр 20 2022, 12:08
Самые активные пользователи за месяц
| Нет пользователей |
Поиск
HM-SHA256-v1. Разные наработки. Часть-1.
Страница 1 из 2 • Поделиться
Страница 1 из 2 • 1, 2 
 HM-SHA256-v1. Разные наработки. Часть-1.
HM-SHA256-v1. Разные наработки. Часть-1.
1
.
Различнные ссылки.
1. http://cryptography.gmu.edu/index.php
2. https://forum.cxem.net/index.php?/topic/158806-получение-хеша-sha256-и-вывод-по-uart-на-atmega16/
3. https://github.com/progranism/Open-Source-FPGA-Bitcoin-Miner.git
4. https://marsohod.org/projects/proekty-dlya-platy-marsokhod3/340-miner-bitcoin
5. https://habr.com/ru/post/318174/
6. https://habr.com/ru/company/selectel/blog/530262/
7. ...
Данную тему можете не читать, она для разработки устройства, просто так удобно и наглядно, хранить мне данные...
.
____Алгоритм использует следующие битовые операции:
ǁ — конкатенация,
+ — сложение,
and — побитовое «И»,
xor — исключающее «ИЛИ»,
shr (shift right) — логический сдвиг вправо,
rotr (rotate right) — циклический сдвиг вправо.
Пояснения:
Все переменные беззнаковые, имеют размер 32 бита и при вычислениях суммируются по модулю 232
message — исходное двоичное сообщение
m — преобразованное сообщение
Инициализация переменных
(первые 32 бита дробных частей квадратных корней первых восьми простых чисел [от 2 до 19]):
h0 := 0x6A09E667
h1 := 0xBB67AE85
h2 := 0x3C6EF372
h3 := 0xA54FF53A
h4 := 0x510E527F
h5 := 0x9B05688C
h6 := 0x1F83D9AB
h7 := 0x5BE0CD19
Таблица констант
(первые 32 бита дробных частей кубических корней первых 64 простых чисел [от 2 до 311]):
k[0..63] :=
0x428A2F98, 0x71374491, 0xB5C0FBCF, 0xE9B5DBA5,
0x3956C25B, 0x59F111F1, 0x923F82A4, 0xAB1C5ED5,
0xD807AA98, 0x12835B01, 0x243185BE, 0x550C7DC3,
0x72BE5D74, 0x80DEB1FE, 0x9BDC06A7, 0xC19BF174,
0xE49B69C1, 0xEFBE4786, 0x0FC19DC6, 0x240CA1CC,
0x2DE92C6F, 0x4A7484AA, 0x5CB0A9DC, 0x76F988DA,
0x983E5152, 0xA831C66D, 0xB00327C8, 0xBF597FC7,
0xC6E00BF3, 0xD5A79147, 0x06CA6351, 0x14292967,
0x27B70A85, 0x2E1B2138, 0x4D2C6DFC, 0x53380D13,
0x650A7354, 0x766A0ABB, 0x81C2C92E, 0x92722C85,
0xA2BFE8A1, 0xA81A664B, 0xC24B8B70, 0xC76C51A3,
0xD192E819, 0xD6990624, 0xF40E3585, 0x106AA070,
0x19A4C116, 0x1E376C08, 0x2748774C, 0x34B0BCB5,
0x391C0CB3, 0x4ED8AA4A, 0x5B9CCA4F, 0x682E6FF3,
0x748F82EE, 0x78A5636F, 0x84C87814, 0x8CC70208,
0x90BEFFFA, 0xA4506CEB, 0xBEF9A3F7, 0xC67178F2
Предварительная обработка:
m := message ǁ [единичный бит]
m := m ǁ [k нулевых бит],
где k — наименьшее неотрицательное число, такое что
(L + 1 + K) mod 512 = 448, где L — число бит в сообщении (сравнима по модулю 512 c 448)
m := m ǁ Длина(message)
- длина исходного сообщения в битах в виде 64-битного числа с порядком байтов от старшего к младшему
Далее сообщение обрабатывается последовательными порциями по 512 бит:
разбить сообщение на куски по 512 бит
для каждого куска разбить кусок на 16 слов длиной 32 бита (с порядком байтов от старшего к младшему внутри слова): w[0..15]
Сгенерировать дополнительные 48 слов:
для i от 16 до 63
s0 := (w[i-15] rotr 7) xor (w[i-15] rotr 18) xor (w[i-15] shr 3)
s1 := (w[i-2] rotr 17) xor (w[i-2] rotr 19) xor (w[i-2] shr 10)
w[i] := w[i-16] + s0 + w[i-7] + s1
Инициализация вспомогательных переменных:
a := h0
b := h1
c := h2
d := h3
e := h4
f := h5
g := h6
h := h7
Основной цикл:
для i от 0 до 63
Σ0 := (a rotr 2) xor (a rotr 13) xor (a rotr 22)
Ma := (a and b) xor (a and c) xor (b and c)
t2 := Σ0 + Ma
Σ1 := (e rotr 6) xor (e rotr 11) xor (e rotr 25)
Ch := (e and f) xor ((not e) and g)
t1 := h + Σ1 + Ch + k[i] + w[i]
h := g
g := f
f := e
e := d + t1
d := c
c := b
b := a
a := t1 + t2
Добавить полученные значения к ранее вычисленному результату:
h0 := h0 + a
h1 := h1 + b
h2 := h2 + c
h3 := h3 + d
h4 := h4 + e
h5 := h5 + f
h6 := h6 + g
h7 := h7 + h
Получить итоговое значение хеша:
digest = hash = h0 ǁ h1 ǁ h2 ǁ h3 ǁ h4 ǁ h5 ǁ h6 ǁ h7
___________________________________________________________________________________________
Полезные ссылки, а может и не очень:
1. https://github.com/JerryWm/Stratum-proxy-SHA256
.
Различнные ссылки.
1. http://cryptography.gmu.edu/index.php
2. https://forum.cxem.net/index.php?/topic/158806-получение-хеша-sha256-и-вывод-по-uart-на-atmega16/
- Спойлер:
- UART
#include <avr/io.h>
#include <avr/delay.h>
void init_UART(void)
{
UBRRH = 0;
UBRRL = 12;
UCSRA=0b00000000;
UCSRB=0b00011100;
UCSRC=0b10000110;
}
void send_Uart(unsigned char c)// Отправка байта
{
while(!(UCSRA & (1 << UDRE))) // Устанавливается, когда регистр свободен
{}
UDR = c;
}
void send_Uart_str(unsigned char *s)// Отправка строки
{
while(*s != 0) send_Uart(*s++);
}
void main(void)
{
DDRD = 0b00010010; // RXD = 0, TXD = 1
init_UART(); // инициализация UART
_delay_ms(1000);
while(1){
if( UCSRA & (1 << UDRE ))
{
send_Uart_str("lalalalalalalalala");
PORTD |= ( 1 << 4 ); // Включаем диод PC0 = 1 = Vcc
_delay_ms(50); // задержка 50мс
// LED off
PORTD &=~ ( 1 << 4 ); // Выключаем диод PC0 = 0 = Vcc
_delay_ms(1000);
}
}
}
3. https://github.com/progranism/Open-Source-FPGA-Bitcoin-Miner.git
4. https://marsohod.org/projects/proekty-dlya-platy-marsokhod3/340-miner-bitcoin
5. https://habr.com/ru/post/318174/
6. https://habr.com/ru/company/selectel/blog/530262/
7. ...
____________________________________________________________________________
Данную тему можете не читать, она для разработки устройства, просто так удобно и наглядно, хранить мне данные...
.
Псевдокод.
____Алгоритм использует следующие битовые операции:
ǁ — конкатенация,
+ — сложение,
and — побитовое «И»,
xor — исключающее «ИЛИ»,
shr (shift right) — логический сдвиг вправо,
rotr (rotate right) — циклический сдвиг вправо.
Пояснения:
Все переменные беззнаковые, имеют размер 32 бита и при вычислениях суммируются по модулю 232
message — исходное двоичное сообщение
m — преобразованное сообщение
Инициализация переменных
(первые 32 бита дробных частей квадратных корней первых восьми простых чисел [от 2 до 19]):
h0 := 0x6A09E667
h1 := 0xBB67AE85
h2 := 0x3C6EF372
h3 := 0xA54FF53A
h4 := 0x510E527F
h5 := 0x9B05688C
h6 := 0x1F83D9AB
h7 := 0x5BE0CD19
Таблица констант
(первые 32 бита дробных частей кубических корней первых 64 простых чисел [от 2 до 311]):
k[0..63] :=
0x428A2F98, 0x71374491, 0xB5C0FBCF, 0xE9B5DBA5,
0x3956C25B, 0x59F111F1, 0x923F82A4, 0xAB1C5ED5,
0xD807AA98, 0x12835B01, 0x243185BE, 0x550C7DC3,
0x72BE5D74, 0x80DEB1FE, 0x9BDC06A7, 0xC19BF174,
0xE49B69C1, 0xEFBE4786, 0x0FC19DC6, 0x240CA1CC,
0x2DE92C6F, 0x4A7484AA, 0x5CB0A9DC, 0x76F988DA,
0x983E5152, 0xA831C66D, 0xB00327C8, 0xBF597FC7,
0xC6E00BF3, 0xD5A79147, 0x06CA6351, 0x14292967,
0x27B70A85, 0x2E1B2138, 0x4D2C6DFC, 0x53380D13,
0x650A7354, 0x766A0ABB, 0x81C2C92E, 0x92722C85,
0xA2BFE8A1, 0xA81A664B, 0xC24B8B70, 0xC76C51A3,
0xD192E819, 0xD6990624, 0xF40E3585, 0x106AA070,
0x19A4C116, 0x1E376C08, 0x2748774C, 0x34B0BCB5,
0x391C0CB3, 0x4ED8AA4A, 0x5B9CCA4F, 0x682E6FF3,
0x748F82EE, 0x78A5636F, 0x84C87814, 0x8CC70208,
0x90BEFFFA, 0xA4506CEB, 0xBEF9A3F7, 0xC67178F2
Предварительная обработка:
m := message ǁ [единичный бит]
m := m ǁ [k нулевых бит],
где k — наименьшее неотрицательное число, такое что
(L + 1 + K) mod 512 = 448, где L — число бит в сообщении (сравнима по модулю 512 c 448)
m := m ǁ Длина(message)
- длина исходного сообщения в битах в виде 64-битного числа с порядком байтов от старшего к младшему
Далее сообщение обрабатывается последовательными порциями по 512 бит:
разбить сообщение на куски по 512 бит
для каждого куска разбить кусок на 16 слов длиной 32 бита (с порядком байтов от старшего к младшему внутри слова): w[0..15]
Сгенерировать дополнительные 48 слов:
для i от 16 до 63
s0 := (w[i-15] rotr 7) xor (w[i-15] rotr 18) xor (w[i-15] shr 3)
s1 := (w[i-2] rotr 17) xor (w[i-2] rotr 19) xor (w[i-2] shr 10)
w[i] := w[i-16] + s0 + w[i-7] + s1
Инициализация вспомогательных переменных:
a := h0
b := h1
c := h2
d := h3
e := h4
f := h5
g := h6
h := h7
Основной цикл:
для i от 0 до 63
Σ0 := (a rotr 2) xor (a rotr 13) xor (a rotr 22)
Ma := (a and b) xor (a and c) xor (b and c)
t2 := Σ0 + Ma
Σ1 := (e rotr 6) xor (e rotr 11) xor (e rotr 25)
Ch := (e and f) xor ((not e) and g)
t1 := h + Σ1 + Ch + k[i] + w[i]
h := g
g := f
f := e
e := d + t1
d := c
c := b
b := a
a := t1 + t2
Добавить полученные значения к ранее вычисленному результату:
h0 := h0 + a
h1 := h1 + b
h2 := h2 + c
h3 := h3 + d
h4 := h4 + e
h5 := h5 + f
h6 := h6 + g
h7 := h7 + h
Получить итоговое значение хеша:
digest = hash = h0 ǁ h1 ǁ h2 ǁ h3 ǁ h4 ǁ h5 ǁ h6 ǁ h7
___________________________________________________________________________________________
Полезные ссылки, а может и не очень:
1. https://github.com/JerryWm/Stratum-proxy-SHA256
.
Последний раз редактировалось: Viktor2312 (Ср Мар 16 2022, 00:07), всего редактировалось 14 раз(а)
Viktor2312- RIP
- Сообщения : 15492
Дата регистрации : 2012-08-10
Возраст : 45
Откуда : Пятигорск
 .
.
2
.
SHA-2 хеш алгоритм.
____В 1993 году NIST впервые опубликовал Стандарт Безопасного Хеша (SHA). В 1995 году этот алгоритм был пересмотрен с целью устранения некоторых начальных недостатков, а в 2001 году были предложены новые алгоритмы хеширования. Это новое семейство алгоритмов хеширования, известное как SHA-2, использует большие дайджест-сообщения, делая их более устойчивыми к возможным атакам и позволяя использовать их с большими блоками данных, вплоть до 2128 бит, например, в случае SHA512. Алгоритм хеширования SHA-2 одинаков для хэш-функций SHA256, SHA224, SHA384 и SHA512, различаясь только размером операндов, векторами инициализации и размером окончательного дайджест-сообщения.
____Далее описывается алгоритм SHA-2, применяемый к хеш-функции SHA256, после чего следует описание хеш-функции SHA512, которая отличается в основном размером операндов, используя 64-битные слова вместо 32-битных. Обратите внимание, что SHA224 и SHA384 вычисляются как SHA256 и SHA512, соответственно, с окончательным значением хеш-функции, усеченным до соответствующего размера, вектор инициализации также отличается.
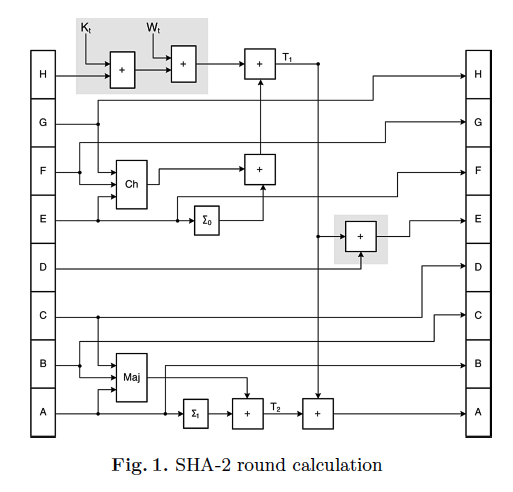
____Функция хеширования SHA256: Функция хеширования SHA256 создает окончательное дайджест-сообщение из 256 битов, которое зависит от входного сообщения и состоит из нескольких блоков по 512 бит в каждом. Этот входной блок расширяется и подается на 64 цикла функции SHA256 в словах по 32 бита каждый (обозначается Wt). В каждом цикле или цикле алгоритма SHA-2 введенные данные смешиваются с текущим состоянием. Это скремблирование данных выполняется с помощью сложений и логических операций, таких как побитовые логические операции и побитовые вращения. Вычислительная структура каждого раунда этого алгоритма изображена на рисунке 1. Несколько функций, представленных на этом рисунке, описаны в Приложении I. Значение Wt является 32-разрядным словом данных для раунда t, а значение Kt представляет 32-битная константа, которая также зависит от раунда.
____32-битные значения переменных от A до H обновляются в каждом раунде, а новые значения используются в следующем раунде. Начальные значения этих переменных задаются 256-битным постоянным значением, указанным в [10], это значение устанавливается только для первого блока данных. В последовательных блоках данных используется промежуточное хеш-значение, вычисленное для предыдущего блока данных. Каждый блок 512 данных обрабатывается в течение 64 циклов, после чего значения переменных от A до H добавляются в предыдущее дайджест-сообщение для получения частичного Дайджест сообщения. Чтобы лучше проиллюстрировать этот алгоритм, представление псевдокода изображено на рисунке 2. Окончательное дайджест-сообщение (DM) для данного потока данных дается результатом последнего блока данных.
____В некоторых приложениях более высокого уровня, таких как эффективная реализация кода аутентификации хеш-сообщения с ключом (HMAC) [11] или когда сообщение фрагментировано, начальное значение хеш-функции (IV) может отличаться от константы, указанной в [10]. В этих случаях переменные от A до H инициализируются переменным вектором инициализации (IV).
____Хеш-функция SHA512: вычисление хеш-функции SHA512 идентично вычислению хеш-функции SHA256, отличающейся размером операндов, которые имеют 64 бита, а не 32 бита, как для SHA256, размера дайджест-сообщения, которое имеет удвоенный размер, составляющий 512 бит, и в функциях, описанных в Приложении I. В этом Приложении также описаны функции, используемые в расписании сообщений. Значения Wt и Kt имеют 64 бита, и каждый блок данных состоит из 16 64-битных слов, имеющих в общей сложности 1024 бита.
____Расписание сообщений: В алгоритме SHA-2 вычисления, описанные на рисунке 1, выполняются для 64 раундов для SHA256 (80 раундов для SHA512), в каждом раунде 32-битное слово (или 64 бита для SHA512), полученное из промежуточного слова. используется хэш-значение Однако каждый блок данных имеет только 16 32-битных слов для SHA256 или 16 64-битных слов для SHA512, что приводит к необходимости расширения исходного блока данных для получения оставшихся слов. Это расширение выполняется вычислением, описанным в (1), где M(i)t обозначает первые 16 слов i-го блока данных.
____Заполнение сообщения: чтобы гарантировать, что входное сообщение кратно 512 битам, как того требует хеш-функция SHA256, или 1024 для хеш-функции SHA512, необходимо дополнить исходное сообщение. Дополненное сообщение состоит из сообщения, с ничего не значащими данными, и присоединённым к нему оригинальным сообщением. Эта операция может быть эффективно реализована в программном обеспечении с минимальными затратами.
Proposed Design.
____В алгоритме SHA-2 операции, которые должны быть выполнены, просты, однако зависимость этого алгоритма от данных не допускает большого распараллеливания. Каждый раунд алгоритма может быть вычислен только после того, как были вычислены значения от A до H предыдущего раунда (см. Рисунок 2), что накладывает последовательность на вычисление. Следует отметить, что в каждом раунде вычисление требуется только для вычисления значений A и E, поскольку остальные значения получаются непосредственно из значений предыдущего раунда, как показано в псевдокоде на рис.2.
____Перепланирование операций: в нашем предложении мы определили часть вычисления данного раунда t, которая может быть вычислена заранее в предыдущем раунде t − 1. Только значения, которые не зависят от значений, вычисленных в предыдущем раунде, могут быть вычислены заранее. В отличие от метода перепланирования, предложенного в [12] для алгоритма SHA1, где взаимная зависимость данных является низкой, в алгоритме SHA-2 зависимость данных является более сложной, как показано на рисунке 1. Хотя переменные B, C, D , F, G и H получены непосредственно из значений раунда, не требующих каких-либо вычислений, значения A и E требуют вычислений и зависят от всех значений. Другими словами, значения A и E для раунда t не могут быть вычислены до тех пор, пока значения для тех же переменных не будут вычислены в предыдущем раунде, как показано в (2).
____Принимая во внимание, что значение Ht + 1 задается непосредственно через Gt, которое, в свою очередь, задается посредством Ft-1, предварительный расчет H, таким образом, может быть задан как Ht + 1 = Ft-1. Поскольку значения Kt и Wt можно предварительно рассчитать и просто использовать в каждом раунде, (2) можно переписать как:
где значение δt рассчитывается в предыдущем раунде. Значение δt + 1 может быть результатом полного сложения или векторов переноса и сохранения из сложения переноса. С этим вычислительным разделением вычисление алгоритма SHA-2 может быть разделено на две части, что позволяет переназначить вычисление δ на предыдущий тактовый цикл, изображенный серой областью на рисунке 3. Таким образом, критический путь результирующего оборудования реализация может быть уменьшена. Поскольку вычисление теперь разделено на этап конвейера, вычисление SHA-2 требует дополнительного тактового цикла для выполнения всех циклов. В случае хэш-функции SHA256 необходимо 65 тактов для расчета 64 раундов. Как указано в алгоритме SHA-2 и изображено на рисунке 2, после вычисления всех циклов внутренние переменные (от A до H) должны быть добавлены к предыдущему дайджест-сообщению.
Пометки:
1. # Майнер отправляет пулу nonce и хеш заданной сложности, пул подставляет этот nonce в заголовки блока и хеширует их, получил в результате тот же хеш - валидный, получил другой хеш - невалидный.
(если я как майнер состоящий в пуле, отсылаю пулу к примеру 100 nonce и соответствующих хешей, то пулл, будет пересчитывать все 100 хешей, что бы провалидировать? Тогда какой от меня смысл, если пул сам может считать эти хеши?)
# Майнер перебирает nonce, чтобы получить "красивый" хеш. Для этого нужно проделать МНОГО операций хеширования.
Пул проверяет, что присланные майнером nonce и хеш соответствуют друг другу. Это ОДНА операция хеширования.
(Как тогда майнинг пул проверит, что я реально работал и сколько работы я проделал, если я не нашел "красивый" хеш, хотя реально искал?)
# Например, сложность выставленная пулом равна 10 000, следовательно майнер будет находить соответствующий хеш в среднем за 10 000 итераций перебора nonce. Ключевое слово - в среднем. Сколько реально было итераций в конкретном случае - сугубо половые пробемы майнера и пулу на это положить, потому что в среднем будет 10 000, не смотря на то, что иной раз его можно найти с первой же итерации, а иногда не найти и за 20 000+ итераций. Как только майнер нашёл соответствующий хеш, он отправляет его и nonce пулу, а пул хеширует у себя и засчитывает майнеру 10 000 итераций. Проще говоря, пулу не нужно проверять сколько майнер сделал работы в каждом конкретном случае, потому что в среднем майнеру придётся перебирать столько, сколько требует заданная сложность, иначе он не найдёт требуемые хеши и отправлять будет нечего.
*задание содержит номер блока, ID задания, хэш предыдущего блока, минимальный и максимальный nonce для тебя
Начальные значения:
h0 := 0x6A09E667 (0110 1010 0000 1001 1110 0110 0110 0111)
h1 := 0xBB67AE85 (1011 1011 0110 0111 1010 1110 1000 0101)
h2 := 0x3C6EF372 (0011 0011 0110 1110 1111 0011 0111 0010)
h3 := 0xA54FF53A (1010 0101 0100 1111 1111 0101 0011 1010)
h4 := 0x510E527F (0101 0001 0000 1110 0101 0010 0111 1111)
h5 := 0x9B05688C (1001 1011 0000 0101 0110 1000 1000 1100)
h6 := 0x1F83D9AB (0001 1111 1000 0011 1101 1001 1010 1011)
h7 := 0x5BE0CD19 (0101 1011 1110 0000 1100 1101 0001 1001)
k0 := 0x428A2F98 (0100 0010 1000 1010 0010 1111 1001 1000)
k1 := 0x71374491 (0111 0001 0011 0111 0100 0100 1001 0001)
k2 := 0xB5C0FBCF (1011 0101 1100 0000 1111 1011 1100 1111)
k3 := 0xE9B5DBA5 (1110 1001 1011 0101 1101 1011 1010 0101)
k4 := 0x3956C25B (0011 1001 0101 0110 1100 0010 0101 1011)
k5 := 0x59F111F1 (0101 1001 1111 0001 0001 0001 1111 0001)
k6 := 0x923F82A4 (1001 0010 0011 1111 1000 0010 1010 0100)
k7 := 0xAB1C5ED5 (1010 1011 0001 1100 0101 1110 1101 0101)
k8 := 0xD807AA98 (1101 1000 0000 0111 1010 1010 1001 1000)
k9 := 0x12835B01 (0001 0010 1000 0011 0101 1011 0000 0001)
k10 := 0x243185BE (0010 0100 0011 0001 1000 0101 1011 1110)
k11 := 0x550C7DC3 (0101 0101 0000 1100 0111 1101 1100 0011)
k12 := 0x72BE5D74 (0111 0010 1011 1110 0101 1101 0111 0111)
k13 := 0x80DEB1FE (1000 0000 1101 1110 1011 0001 1111 1110)
k14 := 0x9BDC06A7 (1001 1011 1101 1100 0000 0110 1010 0111)
k15 := 0xC19BF174 (1100 0001 1001 1011 1111 0001 0111 0100)
Закон дистрибутивности. Дистрибутивность конъюнкции и суммы по модулю два.
(a and b) xor (a and c) = a and (b xor c) !!!
Функция большинства (Ma блок) побитово работает со словами A, B и C. Для каждой битовой позиции она возвращает 0, если большинство входных битов в этой позиции — нули, иначе вернёт 1 (См. Мажоритарный клапан - КР1533ЛП3).
Блок Σ0 циклически сдвигает A на 2 бита, затем исходное слово A циклически сдвигается на 13 бит, и, аналогично, на 22 бита. Получившиеся три сдвинутые версии A побитово складываются по модулю 2 (обычный xor, (A rotr 2) xor (A rotr 13) xor (A rotr 22)).
Ch реализует функцию выбора. На каждой битовой позиции проверяется бит из E, если он равен единице, то на выход идёт бит из F с этой позиции, иначе бит из G. Таким образом, биты из F и G перемешиваются, исходя из значения E.
Σ1 по структуре аналогичен Σ0, но работает со словом E, а соответствующие сдвиговые константы — 6, 11 и 25.
.
SHA-2 хеш алгоритм.
____В 1993 году NIST впервые опубликовал Стандарт Безопасного Хеша (SHA). В 1995 году этот алгоритм был пересмотрен с целью устранения некоторых начальных недостатков, а в 2001 году были предложены новые алгоритмы хеширования. Это новое семейство алгоритмов хеширования, известное как SHA-2, использует большие дайджест-сообщения, делая их более устойчивыми к возможным атакам и позволяя использовать их с большими блоками данных, вплоть до 2128 бит, например, в случае SHA512. Алгоритм хеширования SHA-2 одинаков для хэш-функций SHA256, SHA224, SHA384 и SHA512, различаясь только размером операндов, векторами инициализации и размером окончательного дайджест-сообщения.
____Далее описывается алгоритм SHA-2, применяемый к хеш-функции SHA256, после чего следует описание хеш-функции SHA512, которая отличается в основном размером операндов, используя 64-битные слова вместо 32-битных. Обратите внимание, что SHA224 и SHA384 вычисляются как SHA256 и SHA512, соответственно, с окончательным значением хеш-функции, усеченным до соответствующего размера, вектор инициализации также отличается.
____Функция хеширования SHA256: Функция хеширования SHA256 создает окончательное дайджест-сообщение из 256 битов, которое зависит от входного сообщения и состоит из нескольких блоков по 512 бит в каждом. Этот входной блок расширяется и подается на 64 цикла функции SHA256 в словах по 32 бита каждый (обозначается Wt). В каждом цикле или цикле алгоритма SHA-2 введенные данные смешиваются с текущим состоянием. Это скремблирование данных выполняется с помощью сложений и логических операций, таких как побитовые логические операции и побитовые вращения. Вычислительная структура каждого раунда этого алгоритма изображена на рисунке 1. Несколько функций, представленных на этом рисунке, описаны в Приложении I. Значение Wt является 32-разрядным словом данных для раунда t, а значение Kt представляет 32-битная константа, которая также зависит от раунда.
____32-битные значения переменных от A до H обновляются в каждом раунде, а новые значения используются в следующем раунде. Начальные значения этих переменных задаются 256-битным постоянным значением, указанным в [10], это значение устанавливается только для первого блока данных. В последовательных блоках данных используется промежуточное хеш-значение, вычисленное для предыдущего блока данных. Каждый блок 512 данных обрабатывается в течение 64 циклов, после чего значения переменных от A до H добавляются в предыдущее дайджест-сообщение для получения частичного Дайджест сообщения. Чтобы лучше проиллюстрировать этот алгоритм, представление псевдокода изображено на рисунке 2. Окончательное дайджест-сообщение (DM) для данного потока данных дается результатом последнего блока данных.
____В некоторых приложениях более высокого уровня, таких как эффективная реализация кода аутентификации хеш-сообщения с ключом (HMAC) [11] или когда сообщение фрагментировано, начальное значение хеш-функции (IV) может отличаться от константы, указанной в [10]. В этих случаях переменные от A до H инициализируются переменным вектором инициализации (IV).
____Хеш-функция SHA512: вычисление хеш-функции SHA512 идентично вычислению хеш-функции SHA256, отличающейся размером операндов, которые имеют 64 бита, а не 32 бита, как для SHA256, размера дайджест-сообщения, которое имеет удвоенный размер, составляющий 512 бит, и в функциях, описанных в Приложении I. В этом Приложении также описаны функции, используемые в расписании сообщений. Значения Wt и Kt имеют 64 бита, и каждый блок данных состоит из 16 64-битных слов, имеющих в общей сложности 1024 бита.
____Расписание сообщений: В алгоритме SHA-2 вычисления, описанные на рисунке 1, выполняются для 64 раундов для SHA256 (80 раундов для SHA512), в каждом раунде 32-битное слово (или 64 бита для SHA512), полученное из промежуточного слова. используется хэш-значение Однако каждый блок данных имеет только 16 32-битных слов для SHA256 или 16 64-битных слов для SHA512, что приводит к необходимости расширения исходного блока данных для получения оставшихся слов. Это расширение выполняется вычислением, описанным в (1), где M(i)t обозначает первые 16 слов i-го блока данных.
____Заполнение сообщения: чтобы гарантировать, что входное сообщение кратно 512 битам, как того требует хеш-функция SHA256, или 1024 для хеш-функции SHA512, необходимо дополнить исходное сообщение. Дополненное сообщение состоит из сообщения, с ничего не значащими данными, и присоединённым к нему оригинальным сообщением. Эта операция может быть эффективно реализована в программном обеспечении с минимальными затратами.
Proposed Design.
____В алгоритме SHA-2 операции, которые должны быть выполнены, просты, однако зависимость этого алгоритма от данных не допускает большого распараллеливания. Каждый раунд алгоритма может быть вычислен только после того, как были вычислены значения от A до H предыдущего раунда (см. Рисунок 2), что накладывает последовательность на вычисление. Следует отметить, что в каждом раунде вычисление требуется только для вычисления значений A и E, поскольку остальные значения получаются непосредственно из значений предыдущего раунда, как показано в псевдокоде на рис.2.
____Перепланирование операций: в нашем предложении мы определили часть вычисления данного раунда t, которая может быть вычислена заранее в предыдущем раунде t − 1. Только значения, которые не зависят от значений, вычисленных в предыдущем раунде, могут быть вычислены заранее. В отличие от метода перепланирования, предложенного в [12] для алгоритма SHA1, где взаимная зависимость данных является низкой, в алгоритме SHA-2 зависимость данных является более сложной, как показано на рисунке 1. Хотя переменные B, C, D , F, G и H получены непосредственно из значений раунда, не требующих каких-либо вычислений, значения A и E требуют вычислений и зависят от всех значений. Другими словами, значения A и E для раунда t не могут быть вычислены до тех пор, пока значения для тех же переменных не будут вычислены в предыдущем раунде, как показано в (2).
____Принимая во внимание, что значение Ht + 1 задается непосредственно через Gt, которое, в свою очередь, задается посредством Ft-1, предварительный расчет H, таким образом, может быть задан как Ht + 1 = Ft-1. Поскольку значения Kt и Wt можно предварительно рассчитать и просто использовать в каждом раунде, (2) можно переписать как:
где значение δt рассчитывается в предыдущем раунде. Значение δt + 1 может быть результатом полного сложения или векторов переноса и сохранения из сложения переноса. С этим вычислительным разделением вычисление алгоритма SHA-2 может быть разделено на две части, что позволяет переназначить вычисление δ на предыдущий тактовый цикл, изображенный серой областью на рисунке 3. Таким образом, критический путь результирующего оборудования реализация может быть уменьшена. Поскольку вычисление теперь разделено на этап конвейера, вычисление SHA-2 требует дополнительного тактового цикла для выполнения всех циклов. В случае хэш-функции SHA256 необходимо 65 тактов для расчета 64 раундов. Как указано в алгоритме SHA-2 и изображено на рисунке 2, после вычисления всех циклов внутренние переменные (от A до H) должны быть добавлены к предыдущему дайджест-сообщению.
Пометки:
1. # Майнер отправляет пулу nonce и хеш заданной сложности, пул подставляет этот nonce в заголовки блока и хеширует их, получил в результате тот же хеш - валидный, получил другой хеш - невалидный.
(если я как майнер состоящий в пуле, отсылаю пулу к примеру 100 nonce и соответствующих хешей, то пулл, будет пересчитывать все 100 хешей, что бы провалидировать? Тогда какой от меня смысл, если пул сам может считать эти хеши?)
# Майнер перебирает nonce, чтобы получить "красивый" хеш. Для этого нужно проделать МНОГО операций хеширования.
Пул проверяет, что присланные майнером nonce и хеш соответствуют друг другу. Это ОДНА операция хеширования.
(Как тогда майнинг пул проверит, что я реально работал и сколько работы я проделал, если я не нашел "красивый" хеш, хотя реально искал?)
# Например, сложность выставленная пулом равна 10 000, следовательно майнер будет находить соответствующий хеш в среднем за 10 000 итераций перебора nonce. Ключевое слово - в среднем. Сколько реально было итераций в конкретном случае - сугубо половые пробемы майнера и пулу на это положить, потому что в среднем будет 10 000, не смотря на то, что иной раз его можно найти с первой же итерации, а иногда не найти и за 20 000+ итераций. Как только майнер нашёл соответствующий хеш, он отправляет его и nonce пулу, а пул хеширует у себя и засчитывает майнеру 10 000 итераций. Проще говоря, пулу не нужно проверять сколько майнер сделал работы в каждом конкретном случае, потому что в среднем майнеру придётся перебирать столько, сколько требует заданная сложность, иначе он не найдёт требуемые хеши и отправлять будет нечего.
*задание содержит номер блока, ID задания, хэш предыдущего блока, минимальный и максимальный nonce для тебя
***
Начальные значения:
h0 := 0x6A09E667 (0110 1010 0000 1001 1110 0110 0110 0111)
h1 := 0xBB67AE85 (1011 1011 0110 0111 1010 1110 1000 0101)
h2 := 0x3C6EF372 (0011 0011 0110 1110 1111 0011 0111 0010)
h3 := 0xA54FF53A (1010 0101 0100 1111 1111 0101 0011 1010)
h4 := 0x510E527F (0101 0001 0000 1110 0101 0010 0111 1111)
h5 := 0x9B05688C (1001 1011 0000 0101 0110 1000 1000 1100)
h6 := 0x1F83D9AB (0001 1111 1000 0011 1101 1001 1010 1011)
h7 := 0x5BE0CD19 (0101 1011 1110 0000 1100 1101 0001 1001)
k0 := 0x428A2F98 (0100 0010 1000 1010 0010 1111 1001 1000)
k1 := 0x71374491 (0111 0001 0011 0111 0100 0100 1001 0001)
k2 := 0xB5C0FBCF (1011 0101 1100 0000 1111 1011 1100 1111)
k3 := 0xE9B5DBA5 (1110 1001 1011 0101 1101 1011 1010 0101)
k4 := 0x3956C25B (0011 1001 0101 0110 1100 0010 0101 1011)
k5 := 0x59F111F1 (0101 1001 1111 0001 0001 0001 1111 0001)
k6 := 0x923F82A4 (1001 0010 0011 1111 1000 0010 1010 0100)
k7 := 0xAB1C5ED5 (1010 1011 0001 1100 0101 1110 1101 0101)
k8 := 0xD807AA98 (1101 1000 0000 0111 1010 1010 1001 1000)
k9 := 0x12835B01 (0001 0010 1000 0011 0101 1011 0000 0001)
k10 := 0x243185BE (0010 0100 0011 0001 1000 0101 1011 1110)
k11 := 0x550C7DC3 (0101 0101 0000 1100 0111 1101 1100 0011)
k12 := 0x72BE5D74 (0111 0010 1011 1110 0101 1101 0111 0111)
k13 := 0x80DEB1FE (1000 0000 1101 1110 1011 0001 1111 1110)
k14 := 0x9BDC06A7 (1001 1011 1101 1100 0000 0110 1010 0111)
k15 := 0xC19BF174 (1100 0001 1001 1011 1111 0001 0111 0100)
***
Закон дистрибутивности. Дистрибутивность конъюнкции и суммы по модулю два.
(a and b) xor (a and c) = a and (b xor c) !!!
***
Функция большинства (Ma блок) побитово работает со словами A, B и C. Для каждой битовой позиции она возвращает 0, если большинство входных битов в этой позиции — нули, иначе вернёт 1 (См. Мажоритарный клапан - КР1533ЛП3).
Блок Σ0 циклически сдвигает A на 2 бита, затем исходное слово A циклически сдвигается на 13 бит, и, аналогично, на 22 бита. Получившиеся три сдвинутые версии A побитово складываются по модулю 2 (обычный xor, (A rotr 2) xor (A rotr 13) xor (A rotr 22)).
Ch реализует функцию выбора. На каждой битовой позиции проверяется бит из E, если он равен единице, то на выход идёт бит из F с этой позиции, иначе бит из G. Таким образом, биты из F и G перемешиваются, исходя из значения E.
Σ1 по структуре аналогичен Σ0, но работает со словом E, а соответствующие сдвиговые константы — 6, 11 и 25.
***
.
Последний раз редактировалось: Viktor2312 (Вс Июл 25 2021, 16:58), всего редактировалось 11 раз(а)
Viktor2312- RIP
- Сообщения : 15492
Дата регистрации : 2012-08-10
Возраст : 45
Откуда : Пятигорск
 .
.
3
.
Пометки, отрывки, разное:
.
Пометки, отрывки, разное:
- Спойлер:
- По поводу первых 32 бит, которые должны быть нулями.
.
Последний раз редактировалось: Viktor2312 (Чт Июн 03 2021, 23:53), всего редактировалось 6 раз(а)
Viktor2312- RIP
- Сообщения : 15492
Дата регистрации : 2012-08-10
Возраст : 45
Откуда : Пятигорск
 .
.
4
.
для i от 16 до 63
s0 := (w[i-15] rotr 7) xor (w[i-15] rotr 18) xor (w[i-15] shr 3)
s1 := (w[i-2] rotr 17) xor (w[i-2] rotr 19) xor (w[i-2] shr 10)
w[i] := w[i-16] + s0 + w[i-7] + s1
i = 16
s0 = (w[16-15] rotr 7) xor (w[16-15] rotr 18) xor (w[16-15] shr 3)
s0 = (w[1] rotr 7) xor (w[1] rotr 18) xor (w[1] shr 3)
s1 = (w[16-2] rotr 17) xor (w[16-2] rotr 19) xor (w[16-2] shr 10)
s1 = (w[14] rotr 17) xor (w[14] rotr 19) xor (w[14] shr 10)
w[16] = w[16-16] + s0 + w[16-7] + s1
w[16] = w[0] + s0 + w[9] +s1
Входные слова: w[0], w[1], w[9], w[14]
Выходное слово: w[16]
.
для i от 16 до 63
s0 := (w[i-15] rotr 7) xor (w[i-15] rotr 18) xor (w[i-15] shr 3)
s1 := (w[i-2] rotr 17) xor (w[i-2] rotr 19) xor (w[i-2] shr 10)
w[i] := w[i-16] + s0 + w[i-7] + s1
i = 16
s0 = (w[16-15] rotr 7) xor (w[16-15] rotr 18) xor (w[16-15] shr 3)
s0 = (w[1] rotr 7) xor (w[1] rotr 18) xor (w[1] shr 3)
s1 = (w[16-2] rotr 17) xor (w[16-2] rotr 19) xor (w[16-2] shr 10)
s1 = (w[14] rotr 17) xor (w[14] rotr 19) xor (w[14] shr 10)
w[16] = w[16-16] + s0 + w[16-7] + s1
w[16] = w[0] + s0 + w[9] +s1
Входные слова: w[0], w[1], w[9], w[14]
Выходное слово: w[16]
.
Последний раз редактировалось: Viktor2312 (Чт Май 28 2020, 09:50), всего редактировалось 4 раз(а)
Viktor2312- RIP
- Сообщения : 15492
Дата регистрации : 2012-08-10
Возраст : 45
Откуда : Пятигорск
 .
.
5
Подводим некую черту, этим сообщением. Пора начинать сначала и ближе к практике, хоть всё до конца и не понятно, но многое понятно, те же 64 итерации, их можно уже реализовывать, а всё остальное будет на отдельных, стандартных, платах. Продумав всё, в плане расположения плат, их соединения между собой, частичного параллелизма и асинхронного принципа, опять получается какой-то монстр, так как решено реализовывать на серии 74AC у которой как вроде максимальная тактовая частота в районе 170 МГц, точно нигде не прочитал, но судя по datasheet время задержки распространения находится в районе 1...10 нс, а как оно получится на практике, время покажет. Для того, чтобы передавать на нужную плату 16 слов, это w[0]...w[15] необходимо 16 шлейфов, они будут располагаться сзади и спереди. А так как каждый шлейф занимает 55 мм, то на плате умещается 4 разъёма, с каждой стороны, итого выходит потребуется 4 платы с размерами не менее этих четырёх разъёмов плюс место для разъёма питания и крепления 10 мм, в каждом углу платы. Входные и выходные слова будут находиться слева и справа, чередуясь от платы к плате. Что же выходит, с запада на восток, 4 разъёма (55 * 4 = 220 мм) + крепления (10 *2 = 20 мм), на разъём питания оставим 20 мм и между разъёмами 5 мм промежутки (5 *4 = 20 мм). Итого: 220 + 20 + 20 +20 = 280 мм (28 см). А с юга на север 4 разъёма (55 * 4 = 220 мм) + крепления (10 *2 = 20 мм) и между разъёмами 5 мм промежутки (5 *4 = 20 мм). Итого: 220 + 20 + 20 = 260 мм (26 см). Плат всего 4 шт. на одну итерацию, соответственно 28 + 28 = 56 см и по 10 см расстояние на шлейфы и вентиляцию, 76 см будет ширина, и 26 + 26 = 52 см и по 10 см расстояние на шлейфы и вентиляцию, 72 см это глубина, и минимум 65 слоёв плат, по 2 см на каждую и по 10 см расстояние на вентиляцию и крепления. 65 * 2 = 130 см и + 20 см, итого 150 см.
Вот такие примерные размеры шкафчика 76 х 72 х 150 см. Жуть... Но будет интересно...
Плата A0-0. Условно показаны все разъёмы, но останутся только те, которые действительно нужны будут.

Изменённая ссылка, так как пока по предыдущей у меня ничего не отображается из-за действий преступной организации РКН (роскомпозор).

Ага, преступная организация не спит, и ссылки с http уже тоже не работают, придётся со временем всё дублировать троекратно, как минимум, задали работки на 5 лет вперёд, ну ничего, вечная борьба народа и дорвавшихся, продолжается, та же фотка, но выложенная на Яндексе:
Посмотреть
Твари всё пофигачили, как же они достали, ну ничего, мы с этим идиотизмом ещё поборемся...

Ура ! получилось, спасибо barsik за ссылку, но вот опять же вопрос, вот потрачу год или два и восстановлю, все изображения на форуме, в ручном режиме, добавив под каждым изображением копию на этом ресурсе, и где гарантия, что эта преступная организация не доберётся и до этого ресурса, никакой...
.
Вот такие примерные размеры шкафчика 76 х 72 х 150 см. Жуть... Но будет интересно...
Плата A0-0. Условно показаны все разъёмы, но останутся только те, которые действительно нужны будут.

Изменённая ссылка, так как пока по предыдущей у меня ничего не отображается из-за действий преступной организации РКН (роскомпозор).

Ага, преступная организация не спит, и ссылки с http уже тоже не работают, придётся со временем всё дублировать троекратно, как минимум, задали работки на 5 лет вперёд, ну ничего, вечная борьба народа и дорвавшихся, продолжается, та же фотка, но выложенная на Яндексе:
Посмотреть
Твари всё пофигачили, как же они достали, ну ничего, мы с этим идиотизмом ещё поборемся...

Ура ! получилось, спасибо barsik за ссылку, но вот опять же вопрос, вот потрачу год или два и восстановлю, все изображения на форуме, в ручном режиме, добавив под каждым изображением копию на этом ресурсе, и где гарантия, что эта преступная организация не доберётся и до этого ресурса, никакой...
.
Последний раз редактировалось: Viktor2312 (Чт Май 28 2020, 09:44), всего редактировалось 2 раз(а)
Viktor2312- RIP
- Сообщения : 15492
Дата регистрации : 2012-08-10
Возраст : 45
Откуда : Пятигорск
 НАЧАЛО.
НАЧАЛО.
6
.
____Итак, всё что выше, это либо описание теории самой, по крайней мере самого основного, либо просто предварительное обдумывание. Предварительные наброски, для оценки габаритов, различных затрат и т. д. В результате их стало понятно, что делать майнер по классической схеме, когда делается "в железе" одна итерация, и потом данные гоняются через неё, нет смысла. Для этого нужно брать крутейшую микросхему ПЛИС с техпроцессом 7 нм и на ней всё делать и не факт, что будет круче микросхемы выполненной по технологии ASIC. Да и не готов я это реализовать в полной мере на данный момент, задача немного другая.
____А задача состоит в том, чтобы понять всё, что необходимо для реализации майнера в железе, и на данный момент не всё понятно. А так же обойти различные подводные камни и сделать его супер быстрым. А для этого необходимо реализовать, как минимум все 64 итерации в виде схемы с единым потоком данных, не готов пока на пальцах описать, что имею в виду, но по ходу реализации это станет понятно.
____И на данный момент задачу нашу можно разбить на некоторое количество частей. Первая часть и мы ею будем заниматься потом, это получение данных от пула и отправка ему результатов, пока это всё просто в тумане. Вторая задача, это разбиение полученного message и дополнение. Третья задача, это получение дополнительных слов. И четвёртая создание непосредственно 64-x итераций с подсчётом результатов в первых, начальных, итерациях. И реализовывать это всё будем с конца, так сказать от простого к сложному, по крайней мере по тому, что я уже понял. Хотя уверенности что я всё понял правильно нет вообще никакой, так как информации катастрофически мало, проконсультироваться так же практически не с кем, а те разработчики майнеров, с которыми я общался, например майнера z-enemy, в основном занимаются soft майнерами для GPU, и мало предоставляют полезной информации, по крайней мере понятной для меня на данном итапе развития...
____Дальше, ниже, постепенно будет отображаться процесс разработки, от теории, просчёта, и проектирования, вплоть до железа, в качестве которого пока рассматиривается серия микросхем 74ACxxx. Ну и из предварительных раздумий, стало понятно, что только применение SMD компонентов, абсолютно всех, возможно позволит создать относительно компактное устройство.
____Естественно, если кто-то захочет что-то написать, или проконсультироваться или наоборот помочь, что-то подсказать или поправить увидев явные какие-то ошибки, это очень приветствуется...
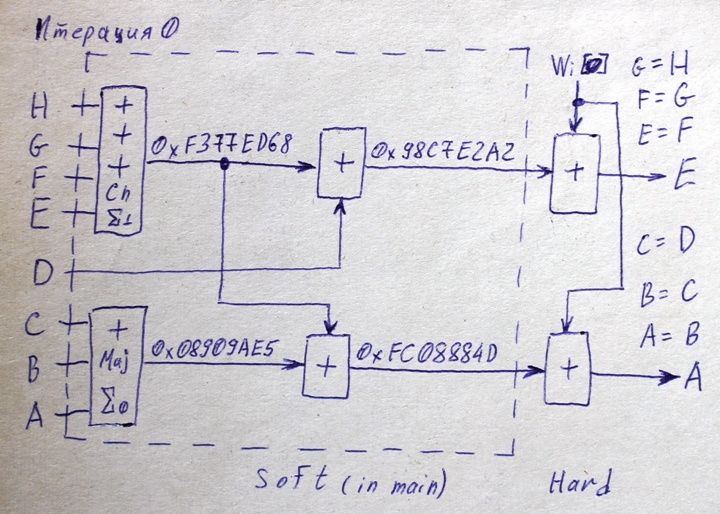
____Итак, ниже представлена структурная схема одной итерации, немного видоизменённая мной, из учёта правила, что от перемены мест слогаемых сумма не меняется, поэтому мы сначала сможем сложить h+Ki, так же сможем сложить Ch+Cy1, здесь Cy1 это вместо значка суммы от слова carry (почему мне вчера пришло на ум именно carry, а не aderr, это всё потому, что не давала покоя проблема переноса. Так как уже было понятно, что 0-я итерация сведётся к двум квантам времени. В первом будет находиться T1, а во втором A и E. И тут возникает проблема, что даже при применении микросхемы CD74ACT283M у которой время выдачи бита переноса занимает 2,7 нс при самых идеальных условиях. А именно, качественный монтаж, питание +5,5 В и исполнение выдерживающее +125 градусов, а так же выдача результата 3,3 нс. И так как этих микросхем для 32-разрядов требуется 8 шт., то имеем, что задержка в первых семи микросхемах будет 2,7 нс, что в сумме составит 18,9 нс и в последней, восьмой, 3,3 нс. А общая минимальная задержка будет 18,9 + 3,3 = 22,2 нс. Что очень медленно, если учесть, что у нас два кванта времени и общая задержка выполнения 0-й итерации будет 44,4 нс. А поэтому нужен полностью параллельный суматор с параллельным переносом на все 32-разряда, либо применение другой, ещё более быстродействующей логики, что не жалательно, либо скорее всего переход от позиционной арифметики к модулярной системе счисления). И сложить полученные значения между собой. В результате потребуется только один сумматор для сложения полученного результата с словом Wi, чтобы получить Т1.

____Хотя, нужно будет проверить идентичность результата, взять любое случайное число Wi и подсчитать результат по старой схеме и по новой, будет ли он совпадать...
Итак, в виду того, что:
Инициализация переменных
(первые 32 бита дробных частей квадратных корней первых восьми простых чисел [от 2 до 19]):
h0 := 0x6A09E667
h1 := 0xBB67AE85
h2 := 0x3C6EF372
h3 := 0xA54FF53A
h4 := 0x510E527F
h5 := 0x9B05688C
h6 := 0x1F83D9AB
h7 := 0x5BE0CD19
Мы имеем начальные фиксированные значения для слов в первой итерации, пардон, в нулевой итерации...
a := h0
b := h1
c := h2
d := h3
e := h4
f := h5
g := h6
h := h7
Мы не будем это всё реализовывать в железе и тратить на это "железо", деньги и время, время на вычисления, каждый раз...
Cy0 = (a rotr 2) xor (a rotr 13) xor (a rotr 22)
a = 0x6A09E667
(a rotr 2) = 0xDA827999
(a rotr 13) = 0x333B504F
(a rotr 22) = 0x27999DA8
0xDA827999 xor 0x333B504F = 0xE9B929D6
Cy0 = 0xE9B929D6 xor 0x27999DA8 = 0xCE20B47E
Для 0-й итерации:
Maj = (a and b) xor (a and c) xor (b and c)
(a and b) = 0x6A09E667 and 0xBB67AE85 = 0x2A01A605
(a and c) = 0x6A09E667 and 0x3C6EF372 = 0x2808E262
(b and c) = 0xBB67AE85 and 0x3C6EF372 = 0x3866A200
0x2A01A605 xor 0x2808E262 = 0x02094467
Maj = 0x02094467 xor 0x3866A200 = 0x3A6FE667
T2 = Maj + Cy0
T2 = 0x08909AE5
____Прежде чем продолжить дальше, нужно проверить закон:
Закон дистрибутивности. Дистрибутивность конъюнкции и суммы по модулю два.
(a and b) xor (a and c) = a and (b xor c) !!!
____Он позволит нам в каждом блоке Maj избавитя от одной операции and, что сэкономит 8 микросхем. Итак преобразуем формулу:
Maj = (a and b) xor (a and c) xor (b and c), в
Maj = (a and (b xor c)) xor (b and c), и посчитаем, получится ли у нас тот же результат:
Maj = (0x6A09E667 and (0xBB67AE85 xor 0x3C6EF372)) xor (0xBB67AE85 and 0x3C6EF372) =
= (0x6A09E667 and 0x87095DF7) xor 0x3866A200 =
= 0x02094467 xor 0x3866A200 = 0x3A6FE667
Результаты совпали, ура, мы сэкономим огромное количество микросхем, а точнее в 126 итерациях по 8 микросхем, то есть 1008 шт. Ну или кучу логических ячеек, при реализации в ПЛИС. То есть не нужно тратить 4032 логических элемента 2И.
Далее вычисляем:
Cy1 = (e rotr 6) xor (e rotr 11) xor (e rotr 25)
h4 := 0x510E527F
e := h4
(0x510E527F rotr 6) = 0xFD443949
(0x510E527F rotr 11) = 0x4FEA21CA
(0x510E527F rotr 25) = 0x87293FA8
0xFD443949 xor 0x4FEA21CA = 0xB2AE1883
0xB2AE1883 xor 0x87293FA8 = 0x3587272B
Cy1 = 0x3587272B
____Далее вычисляем значение на выходе блока Ch:
Ch = (e and f) xor ((not e) and g)
e = 0x510E527F
f = 0x9B05688C
g = 0x1F83D9AB
(not e) = 0xAEF1AD80
Ch = (0x510E527F and 0x9B05688C) xor (0xAEF1AD80 and 0x1F83D9AB) =
= 0x1104400C xor 0x0E818980 = 0x1F85C98C
Ch = 0x1F85C98C
____Находим сумму Adder4:
Adder4 = Ch + Cy1
Adder4 = 0x1F85C98C + 0x3587272B
Adder4 = 0x550CF0B7
____Находим сумму Adder1:
K0 = 0x428A2F98
Adder1 = h + k0
Adder1 = 0x5BE0CD19 + 0x428A2F98
Adder1 = 0x9E6AFCB1
____Находим сумму Adder2:
Adder2 = Adder1 + Adder4
Adder2 = 0x9E6AFCB1 + 0x550CF0B7
Adder2 = 0xF377ED68
____И в итоге, мы имеем полностью просчитанную нулевую итерацию. Остаётся в ней реализовать три "железных" сумматора, для того, чтобы находить T1, A и E. Естественно все вычисления нужно будет ещё раз проверить, и проверить с произвольным Wi внесённые изменения.

____А вот проблема сумматоров теперь максимально остро стоит, нам нужно очень высокое быстродействие, конечно как крайний вариант, это CD74AC283M в количестве 8 шт. для каждого сумматора с максимально достижимым быстродействием в 22,2 нс. в виду того, что между тетрадами у нас последовательный перенос будет. Но, по хорошему нужно рассмотреть реализацию и применение 32-разрядного сумматора не только с параллельным вводом, но и паралельным переносом, хотя бы по 16 бит, в идеале все 32 бита. Но опять же это сильно увеличивает объём "железа", в общим палка о двух концах. Ладно, будем пока потихоньку двигаться дальше и решать проблемы по мере их поступления...
____Проверил, какой результат выдаёт оригинальная схема, например при Wi = 0x3B217FE2 и преобразованная, результаты совпали T1 = 0x2E996D4A, то есть правило "от перемены мест слагаемых сумма не меняется" действует, блин ещё бы ему не действовать, это же 1 класс школы, но просто хотелось убедиться на практике. В общим замечательно, структурная схема со всеми расчётами приведённая выше верная и можно приступать к "железу", хотя бы в теоретическом плане. Модификаций сумматоров будет несколько, скорее всего. Так как наш Adder3, например, имеет константу на одном из входов, а соответственно можно избавиться от 32 контактов, если делать сумматоры в виде отдельной платки, устанавливаемой на основную. Я думаю вы уже поняли, что я хочу сделать не одну итерацию в виде платки и потом с помощью регистров защёлкивать результат и гнать его на вход, подставляя нужные Ki и Wi, а в виде единого потока данных, с одновременной подачей сразу всех Wi для всех 64 итераций, ну да ладно, это не так важно сейчас, посмотрим, что из этого получится, просто по объёму "железа" выходит очень много, ну и пофиг, будем изголяться...
____Сейчас посидел, немного подумал и выходит, что скорость сумматора на CD74AC283M получается переменной, в зависимости от того, есть переносы или нет. В итоге, при определённых числах на входе, когда все переносы равны нулю, то есть их нет, то результат будет валидным уже через 3,3 нс, и самый идеальный вариант, что и в других двух сумматорах, которые работают параллельно, будет такая же ситуация. Тогда время вычисления 0-й итерации будет 6,6 нс, но это, самое максимальное быстродействие при определённых значениях входных переменных, ну а максимальный-идеальный остаётся прежним 44,4 нс. В общим пока ковыряю параллельный сумматор, с параллельным переносом на отдельных логических элементах, просто возможно получися уменьшить количество "железа" в силу того, что у нас одна из переменных имеет определённое значение, а соответственно внутри сумматора, в случае бита слагаемого равного нулю, элемент XOR превращается в повторитель и таким образом его можно вообще убрать из схемы, задержка становится равной 0 нс, да и потребление 0.
____Ну вот, день прошёл не зря, удалось заменить в первой тетраде микросхему CD74AC283M то есть полный 4-разрядный сумматор, у которого время выдачи результата 3,3 нс, а время выдачи бита переноса 2,7 нс, на схему на логических элементах, ну точнее элементе. Потребовался всего один логический элемент НЕ (not) от микросхемы SN74AC04. А это соответственно снижение потребляемой мощности, конкретно этим участком схемы, а также увеличение быстродействия, теперь бит переноса выдаётся за 0 нс, а результат за 1 нс.

____Удалось это сделать конечно только благодаря тому, что одно из слагаемых является константой у нас это число 0x8 (1000), Ну а второе естественно может иметь 16 значений от 0000 до 1111.
____В результате разработки сумматора для следующей тетрады, для битов от I0WI4...I0WI7 задержка распространения, минимально достижимая, вышла 3 нс, а вот количество элементов больше 1...2 корпусов микросхем. Поэтому решил, что проще поставить обычный сумматор, в идеале CD74ACT283 но его нужно будет искать в исполнении на 125 градусов и питать напряжением +5,5 В. Так как в datasheet именно при этих двух параметрах можно получить максимальное быстродействие, то есть минимальные задержки, а именно выдача результата через 3,3 нс и бита переноса через 2,7 нс. В нашем же случае, мы для получения результата будем использовать сумматор, а бит переноса получать не за 2,7 нс взяв его с самой микросхемы, а получать его отдельно при помощи двух логических элементов ИЛИ (or) и И (and), что даёт нам время задержки 2 нс. Таким образом по 8 битам мы имеем, время выдачи результата, через 3,3 нс, а не 6 нс и бит переноса С2 через 2 нс, а не через 5,4 нс.

____Хе хе, а вот и не правильно, я забыл просчитать, если бит переноса из первой тетрады равен 1, то схема уже не пашет на этих двух лог. элементах. Так что во второй тетраде полностью будет задействована микросхема сумматора, и время задержек - результат через 3,3 нс, бит переноса С2 через 2,7 нс.

____Да, медленно. Выход только один, параллельный сумматор, с параллельным переносом на все 32 бита. Тут проще взять формулу в базисе логического элемента И-НЕ (nand) и преобразовать в соответствии с быстродействием конкретных микросхем, например та же ЛА3 от TI имеет минимально достижимую задержку 1,5 нс, в то время как ЛА4 - 1 нс, если судить по datasheet, да меньше на один логический элемент, но тут уже и 1 нс кажется огромной задержкой... В общим, нужно начинать просчитывать полностью с параллельным переносом сумматор. Вся проблема, что больше 8 входов как вроде нет ЛА2 а нужно и с 32 входами И-НЕ элемент, а это только при помощи наращивания и дополнительные ступени, опять же дополнительные 1...2 нс. Но, всё равно выигрыш, пусть даже 3 ступени, и каждая по 1 нс, то это 3 нс, 1 нс в сумматоре, всего 4 нс, против 22,2 нс, в общим... Нужно мучить формулу, чертить схему, с учётом что оба операнда не константы, и будет точно уже потом ясно, где константы, там понятно, всё проще и компактнее...
Где бы ещё время взять, работа, ремонт, пустой холодильник, да и спать иногда желательно...
Ладно, фигня это всё, есть над чем поработать, поразмыслить, что поковырять, больше беспокоит, не приведёт ли ёмкость и индуктивность монтажа, паразитные наводки и весь остальной гемор, к тому, что будет всё с параметрами не min, и даже не typ, а max и тогда это печально, так как это даже не уровень К531 серии будет, у которой в среднем 5...7 нс. Но думаю, коли уж К531 серия в середине 70-х позволяла 5...7 нс, то уж 74ACxxx с SMD монтажом и корпусами, да и платы покачественнее на пару порядков, должны справиться... Слишком много неизвестных...
Ладно, это так, мысли в слух, поживём посмотрим, как оно пойдёт дальше, впереди слишком много ещё работы...
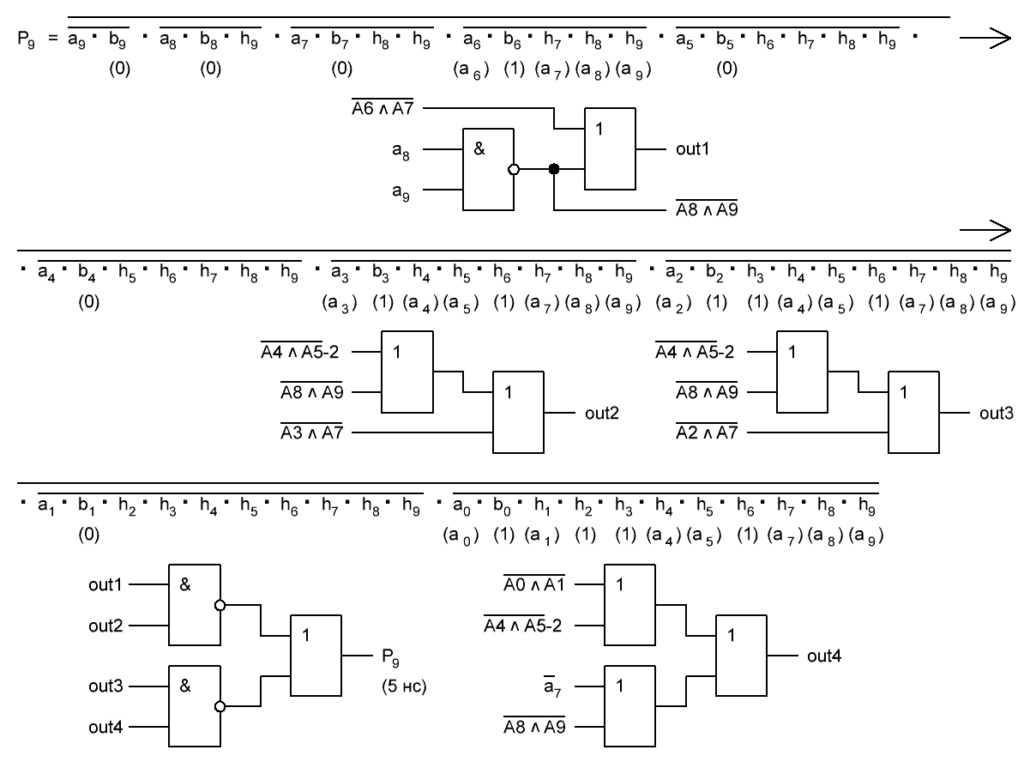
Итак, делаем параллельный сумматор с параллельным переносом для Adder3 первые 4 бита у нас готовы, следующий бит I0ADD3OUT4 требует одного элемента "исключающее ИЛИ" (XOR), на один вход подаётся четвёртый бит слова, а на второй третий бит слова, так как формула переноса полностью коллапсирует до повторителя для P3 (Пэ три):
P3 = / /ai . bi . /ai-1 . bi-1 . hi-1 . /ai-2 . bi-2 . hi-1 . hi . /ai-3 . bi-3 . hi-2 . hi-1 . hi . /p . h0 . h1 . h2 . h3
Как видим /ai . bi
это для P3
/a3 . b3
а b3 = 1 соответственно наш логический элемент 2И-НЕ имеет на одном из входов константу равную всегда лог.1 и соответственно элемент становится просто инвертором. Во всех остальных частях формулы у нас присутствуют p, b0, b1, b2 которые так же константы и равны лог. 0 из-за чего каждый из этих элементов всегда на выходе имеет константу равную лог. 1, соответственно общая инверсия, то есть по сути это логический элемент 5И-НЕ, становится инвертором для /a3 . b3 и поэтому нет смысла пропускать сигнал a3 через два последовательно включённых инвертора, поэтому он у нас приходит на прямую на сумматор, который так же упрощается до одного логического элемента XOR...
Процесс потихоньку идёт, просчитал 8 бит, получилось компактненько, 4 корпуса микросхем и то есть ещё 5 свободных логических элемента и задержка пока что составляет 3 нс, естественно минимально достижимая при различных условиях, оговоренных выше, т. е. питание 5,5 В, и т. д. Продолжу просчитывать дальше на днях по мере появления свободного времени.

Итак, сегодня (18.06.2020г.) выдался свободный денёк, и можно плотно заняться сумматором Adder3. И пожалуй придётся начать всё сначала, так как во-первых, у меня образовалась приличная пачка черновиков, в которых уже сам чёрт ногу сломи, и когда я недавно накосяпорил в схеме, то восстановить её по черновикам с налёту не смог. А во-вторых в процессе восстановления пришла мысль, что можно ещё прилично сократить объём используемых логических элементов. И это всё потому, что второе слагаемое у нас константа с точно известным значением каждого бита. Да и заодно можно будет всё детально и тщательно проверить. К томуже, нужно всё же, с черновиков переносить данные в электронный вид, и удобочитаемый, чтобы можно было в любой момент вернуться назад и посмотреть, да и при проверке так будет гораздо удобнее, а точнее по сути, просто возможно. Поэтому переберусь я в пост ниже и там потихоньку начну...
.
Начало разработки.
____Итак, всё что выше, это либо описание теории самой, по крайней мере самого основного, либо просто предварительное обдумывание. Предварительные наброски, для оценки габаритов, различных затрат и т. д. В результате их стало понятно, что делать майнер по классической схеме, когда делается "в железе" одна итерация, и потом данные гоняются через неё, нет смысла. Для этого нужно брать крутейшую микросхему ПЛИС с техпроцессом 7 нм и на ней всё делать и не факт, что будет круче микросхемы выполненной по технологии ASIC. Да и не готов я это реализовать в полной мере на данный момент, задача немного другая.
____А задача состоит в том, чтобы понять всё, что необходимо для реализации майнера в железе, и на данный момент не всё понятно. А так же обойти различные подводные камни и сделать его супер быстрым. А для этого необходимо реализовать, как минимум все 64 итерации в виде схемы с единым потоком данных, не готов пока на пальцах описать, что имею в виду, но по ходу реализации это станет понятно.
____И на данный момент задачу нашу можно разбить на некоторое количество частей. Первая часть и мы ею будем заниматься потом, это получение данных от пула и отправка ему результатов, пока это всё просто в тумане. Вторая задача, это разбиение полученного message и дополнение. Третья задача, это получение дополнительных слов. И четвёртая создание непосредственно 64-x итераций с подсчётом результатов в первых, начальных, итерациях. И реализовывать это всё будем с конца, так сказать от простого к сложному, по крайней мере по тому, что я уже понял. Хотя уверенности что я всё понял правильно нет вообще никакой, так как информации катастрофически мало, проконсультироваться так же практически не с кем, а те разработчики майнеров, с которыми я общался, например майнера z-enemy, в основном занимаются soft майнерами для GPU, и мало предоставляют полезной информации, по крайней мере понятной для меня на данном итапе развития...
____Дальше, ниже, постепенно будет отображаться процесс разработки, от теории, просчёта, и проектирования, вплоть до железа, в качестве которого пока рассматиривается серия микросхем 74ACxxx. Ну и из предварительных раздумий, стало понятно, что только применение SMD компонентов, абсолютно всех, возможно позволит создать относительно компактное устройство.
____Естественно, если кто-то захочет что-то написать, или проконсультироваться или наоборот помочь, что-то подсказать или поправить увидев явные какие-то ошибки, это очень приветствуется...
____Итак, ниже представлена структурная схема одной итерации, немного видоизменённая мной, из учёта правила, что от перемены мест слогаемых сумма не меняется, поэтому мы сначала сможем сложить h+Ki, так же сможем сложить Ch+Cy1, здесь Cy1 это вместо значка суммы от слова carry (почему мне вчера пришло на ум именно carry, а не aderr, это всё потому, что не давала покоя проблема переноса. Так как уже было понятно, что 0-я итерация сведётся к двум квантам времени. В первом будет находиться T1, а во втором A и E. И тут возникает проблема, что даже при применении микросхемы CD74ACT283M у которой время выдачи бита переноса занимает 2,7 нс при самых идеальных условиях. А именно, качественный монтаж, питание +5,5 В и исполнение выдерживающее +125 градусов, а так же выдача результата 3,3 нс. И так как этих микросхем для 32-разрядов требуется 8 шт., то имеем, что задержка в первых семи микросхемах будет 2,7 нс, что в сумме составит 18,9 нс и в последней, восьмой, 3,3 нс. А общая минимальная задержка будет 18,9 + 3,3 = 22,2 нс. Что очень медленно, если учесть, что у нас два кванта времени и общая задержка выполнения 0-й итерации будет 44,4 нс. А поэтому нужен полностью параллельный суматор с параллельным переносом на все 32-разряда, либо применение другой, ещё более быстродействующей логики, что не жалательно, либо скорее всего переход от позиционной арифметики к модулярной системе счисления). И сложить полученные значения между собой. В результате потребуется только один сумматор для сложения полученного результата с словом Wi, чтобы получить Т1.

____Хотя, нужно будет проверить идентичность результата, взять любое случайное число Wi и подсчитать результат по старой схеме и по новой, будет ли он совпадать...
Итак, в виду того, что:
Инициализация переменных
(первые 32 бита дробных частей квадратных корней первых восьми простых чисел [от 2 до 19]):
h0 := 0x6A09E667
h1 := 0xBB67AE85
h2 := 0x3C6EF372
h3 := 0xA54FF53A
h4 := 0x510E527F
h5 := 0x9B05688C
h6 := 0x1F83D9AB
h7 := 0x5BE0CD19
Мы имеем начальные фиксированные значения для слов в первой итерации, пардон, в нулевой итерации...
a := h0
b := h1
c := h2
d := h3
e := h4
f := h5
g := h6
h := h7
Мы не будем это всё реализовывать в железе и тратить на это "железо", деньги и время, время на вычисления, каждый раз...
Cy0 = (a rotr 2) xor (a rotr 13) xor (a rotr 22)
a = 0x6A09E667
(a rotr 2) = 0xDA827999
(a rotr 13) = 0x333B504F
(a rotr 22) = 0x27999DA8
0xDA827999 xor 0x333B504F = 0xE9B929D6
Cy0 = 0xE9B929D6 xor 0x27999DA8 = 0xCE20B47E
Для 0-й итерации:
Maj = (a and b) xor (a and c) xor (b and c)
(a and b) = 0x6A09E667 and 0xBB67AE85 = 0x2A01A605
(a and c) = 0x6A09E667 and 0x3C6EF372 = 0x2808E262
(b and c) = 0xBB67AE85 and 0x3C6EF372 = 0x3866A200
0x2A01A605 xor 0x2808E262 = 0x02094467
Maj = 0x02094467 xor 0x3866A200 = 0x3A6FE667
T2 = Maj + Cy0
T2 = 0x08909AE5
____Прежде чем продолжить дальше, нужно проверить закон:
Закон дистрибутивности. Дистрибутивность конъюнкции и суммы по модулю два.
(a and b) xor (a and c) = a and (b xor c) !!!
____Он позволит нам в каждом блоке Maj избавитя от одной операции and, что сэкономит 8 микросхем. Итак преобразуем формулу:
Maj = (a and b) xor (a and c) xor (b and c), в
Maj = (a and (b xor c)) xor (b and c), и посчитаем, получится ли у нас тот же результат:
Maj = (0x6A09E667 and (0xBB67AE85 xor 0x3C6EF372)) xor (0xBB67AE85 and 0x3C6EF372) =
= (0x6A09E667 and 0x87095DF7) xor 0x3866A200 =
= 0x02094467 xor 0x3866A200 = 0x3A6FE667
Результаты совпали, ура, мы сэкономим огромное количество микросхем, а точнее в 126 итерациях по 8 микросхем, то есть 1008 шт. Ну или кучу логических ячеек, при реализации в ПЛИС. То есть не нужно тратить 4032 логических элемента 2И.
Далее вычисляем:
Cy1 = (e rotr 6) xor (e rotr 11) xor (e rotr 25)
h4 := 0x510E527F
e := h4
(0x510E527F rotr 6) = 0xFD443949
(0x510E527F rotr 11) = 0x4FEA21CA
(0x510E527F rotr 25) = 0x87293FA8
0xFD443949 xor 0x4FEA21CA = 0xB2AE1883
0xB2AE1883 xor 0x87293FA8 = 0x3587272B
Cy1 = 0x3587272B
____Далее вычисляем значение на выходе блока Ch:
Ch = (e and f) xor ((not e) and g)
e = 0x510E527F
f = 0x9B05688C
g = 0x1F83D9AB
(not e) = 0xAEF1AD80
Ch = (0x510E527F and 0x9B05688C) xor (0xAEF1AD80 and 0x1F83D9AB) =
= 0x1104400C xor 0x0E818980 = 0x1F85C98C
Ch = 0x1F85C98C
____Находим сумму Adder4:
Adder4 = Ch + Cy1
Adder4 = 0x1F85C98C + 0x3587272B
Adder4 = 0x550CF0B7
____Находим сумму Adder1:
K0 = 0x428A2F98
Adder1 = h + k0
Adder1 = 0x5BE0CD19 + 0x428A2F98
Adder1 = 0x9E6AFCB1
____Находим сумму Adder2:
Adder2 = Adder1 + Adder4
Adder2 = 0x9E6AFCB1 + 0x550CF0B7
Adder2 = 0xF377ED68
____И в итоге, мы имеем полностью просчитанную нулевую итерацию. Остаётся в ней реализовать три "железных" сумматора, для того, чтобы находить T1, A и E. Естественно все вычисления нужно будет ещё раз проверить, и проверить с произвольным Wi внесённые изменения.

____А вот проблема сумматоров теперь максимально остро стоит, нам нужно очень высокое быстродействие, конечно как крайний вариант, это CD74AC283M в количестве 8 шт. для каждого сумматора с максимально достижимым быстродействием в 22,2 нс. в виду того, что между тетрадами у нас последовательный перенос будет. Но, по хорошему нужно рассмотреть реализацию и применение 32-разрядного сумматора не только с параллельным вводом, но и паралельным переносом, хотя бы по 16 бит, в идеале все 32 бита. Но опять же это сильно увеличивает объём "железа", в общим палка о двух концах. Ладно, будем пока потихоньку двигаться дальше и решать проблемы по мере их поступления...
____Проверил, какой результат выдаёт оригинальная схема, например при Wi = 0x3B217FE2 и преобразованная, результаты совпали T1 = 0x2E996D4A, то есть правило "от перемены мест слагаемых сумма не меняется" действует, блин ещё бы ему не действовать, это же 1 класс школы, но просто хотелось убедиться на практике. В общим замечательно, структурная схема со всеми расчётами приведённая выше верная и можно приступать к "железу", хотя бы в теоретическом плане. Модификаций сумматоров будет несколько, скорее всего. Так как наш Adder3, например, имеет константу на одном из входов, а соответственно можно избавиться от 32 контактов, если делать сумматоры в виде отдельной платки, устанавливаемой на основную. Я думаю вы уже поняли, что я хочу сделать не одну итерацию в виде платки и потом с помощью регистров защёлкивать результат и гнать его на вход, подставляя нужные Ki и Wi, а в виде единого потока данных, с одновременной подачей сразу всех Wi для всех 64 итераций, ну да ладно, это не так важно сейчас, посмотрим, что из этого получится, просто по объёму "железа" выходит очень много, ну и пофиг, будем изголяться...
____Сейчас посидел, немного подумал и выходит, что скорость сумматора на CD74AC283M получается переменной, в зависимости от того, есть переносы или нет. В итоге, при определённых числах на входе, когда все переносы равны нулю, то есть их нет, то результат будет валидным уже через 3,3 нс, и самый идеальный вариант, что и в других двух сумматорах, которые работают параллельно, будет такая же ситуация. Тогда время вычисления 0-й итерации будет 6,6 нс, но это, самое максимальное быстродействие при определённых значениях входных переменных, ну а максимальный-идеальный остаётся прежним 44,4 нс. В общим пока ковыряю параллельный сумматор, с параллельным переносом на отдельных логических элементах, просто возможно получися уменьшить количество "железа" в силу того, что у нас одна из переменных имеет определённое значение, а соответственно внутри сумматора, в случае бита слагаемого равного нулю, элемент XOR превращается в повторитель и таким образом его можно вообще убрать из схемы, задержка становится равной 0 нс, да и потребление 0.
____Ну вот, день прошёл не зря, удалось заменить в первой тетраде микросхему CD74AC283M то есть полный 4-разрядный сумматор, у которого время выдачи результата 3,3 нс, а время выдачи бита переноса 2,7 нс, на схему на логических элементах, ну точнее элементе. Потребовался всего один логический элемент НЕ (not) от микросхемы SN74AC04. А это соответственно снижение потребляемой мощности, конкретно этим участком схемы, а также увеличение быстродействия, теперь бит переноса выдаётся за 0 нс, а результат за 1 нс.

____Удалось это сделать конечно только благодаря тому, что одно из слагаемых является константой у нас это число 0x8 (1000), Ну а второе естественно может иметь 16 значений от 0000 до 1111.
____В результате разработки сумматора для следующей тетрады, для битов от I0WI4...I0WI7 задержка распространения, минимально достижимая, вышла 3 нс, а вот количество элементов больше 1...2 корпусов микросхем. Поэтому решил, что проще поставить обычный сумматор, в идеале CD74ACT283 но его нужно будет искать в исполнении на 125 градусов и питать напряжением +5,5 В. Так как в datasheet именно при этих двух параметрах можно получить максимальное быстродействие, то есть минимальные задержки, а именно выдача результата через 3,3 нс и бита переноса через 2,7 нс. В нашем же случае, мы для получения результата будем использовать сумматор, а бит переноса получать не за 2,7 нс взяв его с самой микросхемы, а получать его отдельно при помощи двух логических элементов ИЛИ (or) и И (and), что даёт нам время задержки 2 нс. Таким образом по 8 битам мы имеем, время выдачи результата, через 3,3 нс, а не 6 нс и бит переноса С2 через 2 нс, а не через 5,4 нс.

____Хе хе, а вот и не правильно, я забыл просчитать, если бит переноса из первой тетрады равен 1, то схема уже не пашет на этих двух лог. элементах. Так что во второй тетраде полностью будет задействована микросхема сумматора, и время задержек - результат через 3,3 нс, бит переноса С2 через 2,7 нс.

____Да, медленно. Выход только один, параллельный сумматор, с параллельным переносом на все 32 бита. Тут проще взять формулу в базисе логического элемента И-НЕ (nand) и преобразовать в соответствии с быстродействием конкретных микросхем, например та же ЛА3 от TI имеет минимально достижимую задержку 1,5 нс, в то время как ЛА4 - 1 нс, если судить по datasheet, да меньше на один логический элемент, но тут уже и 1 нс кажется огромной задержкой... В общим, нужно начинать просчитывать полностью с параллельным переносом сумматор. Вся проблема, что больше 8 входов как вроде нет ЛА2 а нужно и с 32 входами И-НЕ элемент, а это только при помощи наращивания и дополнительные ступени, опять же дополнительные 1...2 нс. Но, всё равно выигрыш, пусть даже 3 ступени, и каждая по 1 нс, то это 3 нс, 1 нс в сумматоре, всего 4 нс, против 22,2 нс, в общим... Нужно мучить формулу, чертить схему, с учётом что оба операнда не константы, и будет точно уже потом ясно, где константы, там понятно, всё проще и компактнее...
Где бы ещё время взять, работа, ремонт, пустой холодильник, да и спать иногда желательно...
Ладно, фигня это всё, есть над чем поработать, поразмыслить, что поковырять, больше беспокоит, не приведёт ли ёмкость и индуктивность монтажа, паразитные наводки и весь остальной гемор, к тому, что будет всё с параметрами не min, и даже не typ, а max и тогда это печально, так как это даже не уровень К531 серии будет, у которой в среднем 5...7 нс. Но думаю, коли уж К531 серия в середине 70-х позволяла 5...7 нс, то уж 74ACxxx с SMD монтажом и корпусами, да и платы покачественнее на пару порядков, должны справиться... Слишком много неизвестных...
Ладно, это так, мысли в слух, поживём посмотрим, как оно пойдёт дальше, впереди слишком много ещё работы...
Итак, делаем параллельный сумматор с параллельным переносом для Adder3 первые 4 бита у нас готовы, следующий бит I0ADD3OUT4 требует одного элемента "исключающее ИЛИ" (XOR), на один вход подаётся четвёртый бит слова, а на второй третий бит слова, так как формула переноса полностью коллапсирует до повторителя для P3 (Пэ три):
P3 = / /ai . bi . /ai-1 . bi-1 . hi-1 . /ai-2 . bi-2 . hi-1 . hi . /ai-3 . bi-3 . hi-2 . hi-1 . hi . /p . h0 . h1 . h2 . h3
Как видим /ai . bi
это для P3
/a3 . b3
а b3 = 1 соответственно наш логический элемент 2И-НЕ имеет на одном из входов константу равную всегда лог.1 и соответственно элемент становится просто инвертором. Во всех остальных частях формулы у нас присутствуют p, b0, b1, b2 которые так же константы и равны лог. 0 из-за чего каждый из этих элементов всегда на выходе имеет константу равную лог. 1, соответственно общая инверсия, то есть по сути это логический элемент 5И-НЕ, становится инвертором для /a3 . b3 и поэтому нет смысла пропускать сигнал a3 через два последовательно включённых инвертора, поэтому он у нас приходит на прямую на сумматор, который так же упрощается до одного логического элемента XOR...
Процесс потихоньку идёт, просчитал 8 бит, получилось компактненько, 4 корпуса микросхем и то есть ещё 5 свободных логических элемента и задержка пока что составляет 3 нс, естественно минимально достижимая при различных условиях, оговоренных выше, т. е. питание 5,5 В, и т. д. Продолжу просчитывать дальше на днях по мере появления свободного времени.

Итак, сегодня (18.06.2020г.) выдался свободный денёк, и можно плотно заняться сумматором Adder3. И пожалуй придётся начать всё сначала, так как во-первых, у меня образовалась приличная пачка черновиков, в которых уже сам чёрт ногу сломи, и когда я недавно накосяпорил в схеме, то восстановить её по черновикам с налёту не смог. А во-вторых в процессе восстановления пришла мысль, что можно ещё прилично сократить объём используемых логических элементов. И это всё потому, что второе слагаемое у нас константа с точно известным значением каждого бита. Да и заодно можно будет всё детально и тщательно проверить. К томуже, нужно всё же, с черновиков переносить данные в электронный вид, и удобочитаемый, чтобы можно было в любой момент вернуться назад и посмотреть, да и при проверке так будет гораздо удобнее, а точнее по сути, просто возможно. Поэтому переберусь я в пост ниже и там потихоньку начну...
.
Последний раз редактировалось: Viktor2312 (Чт Июн 18 2020, 09:12), всего редактировалось 40 раз(а)
Viktor2312- RIP
- Сообщения : 15492
Дата регистрации : 2012-08-10
Возраст : 45
Откуда : Пятигорск
 .
.
7
.
Поехали...
Итак, мы имеем сумматор, который имеет два 32-разрядных входа и один 32-разрядный выход. Первое слагаемое a, это переменная, а точнее слово w[0]. Второе слагаемое b, это константа с точно известным значением, а именно 0хF377ED68. А соответственно по сути у нас получается преобразователь данных, есть вход, на который подаётся переменная a и есть вход, на котором получается значение T1. Для начала запишем наше число в двоичной форме, пожалуй это будет лучше сделать в графическом виде, я для этого использую программу Splan в которой я черчу схемы и вообще всё, что угодно, так как более простой в освоении программы, мне потребовался 1 час, чтобы разобраться в ней, и удобной в использовании, я ещё не встречал. Ну а потом просто конвертирую в .bmp формат, для этого в ней имеется кнопочка, пойду почерчу...
Готово, загрузим, а нет не загрузим, у нас как всегда ipic.su не доступен Error 521 Web server is down, как же это за..бало, но мы пойдём другим путём...

Все нервы измотали, но как вроде нашёл, куда грузится и работает vfl.ru
Итак, хух, на рисунке выше наше входное слово b, теперь оно представлено наглядно и всегда можно посмотреть какой бит чему равен. Для нас максимально выгодно, чтобы в нём, да и в любом другом было как можно больше нулей, это кардинально сокращает количество "железа", но что имеем, то имеем, с этим и будем работать. Так же нам здесь очень везёт, что входной бит переноса из младшего разряда p не используется и по сути всегда равен нулю, это вообще отрезает огромный кусок схемы и не только тут, но и в дальнейшем, где оба слагаемых будут переменными. Далее представим нашу формулу, опять чертить...

Как видим в последней части формулы у нас присутствует бит переноса из младшего разряда p, а он у нас всегда равен нулю, соответственно присутствуя на входе логического элемента И-НЕ он создаёт условие, что у нас на выходе этого логического элемента всегда будет лог. 1 и таким образом, нет смысла реализовывать данный логический элемент в "железе", достаточно просто подать лог. 1 на вход следующего элемента И-НЕ, но и это не нужно делать, так как лог. 1 на многовходовом логическом элементе И-НЕ, если она константа и всегда равна лог. 1, просто убирает данный вход. Например, если у нас логический элемент 4И-НЕ и на один из входов постоянно подаётся лог. 1, то он просто превращается в логический элемент 3И-НЕ. Таким образом последняя часть формулы отпадает во всех случаях, вне зависимости от того, обе переменные у нас на входе сумматора или одна из них равна константе, так как входной бит переноса из младшего разряда у нас всегда равен лог.0. Далее перейдём к реализации, а точнее проверки 0-го бита нашего сумматора. Итак, мы имеем вход a значение которого мы не знаем и вход b значение которого мы знаем. Так как мы расчитываем 0-й бит, то и входные слагаемые у нас a0 и b0, входной бит переноса равен нулю. Для этого нам нужно вычертить схему одного разряда сумматора, и она будет идентичная для всех разрядов, и самое главное, что в ней нам не требуется реализовывать выходной бит переноса, так как у нас параллельный сумматор с параллельным переносом, пойду почерчу, не я конечно пойду кофе пить и курить, а потом...
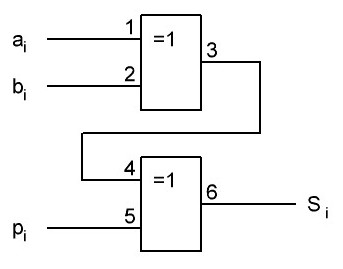
Вот и наш сумматор, схема в данном случае универсальная, для всех разрядов, то есть, если бы у нас на обоих входах были переменные, а так и будет в последующих итерациях, то для 32 разрядов требуется 16 микросхем SN74AC86D которая содержит 4 логических элемента "исключающее ИЛИ" (xor), по два логических элемента на один разряд. Но в данном конкретном нулевом разряде у нас p=0, также b0=0. И тут у нас получается хорошая возможность сократить количество "железа", так как известно, что если на одном из входов логического элемента "исключающее ИЛИ" присутствует константа лог. 1, то элемент становится инвертором, а если лог. 0, то повторителем. Это легко проверить по таблице истиности или по самому свойству данного логического элемента, так как это сумматор, но без бита переноса в старший разряд:
0 + 0 = 0; 0 + 1 = 1; 1 + 0 = 1; 1 + 1 =0 В последнем случае еденица переходит в старший разряд, но так как у элемента xor она отбрасывается, то и получается 1 + 1 = 0.
Теперь как видим если у нас b0=0, то есть будет два возможных варианта a0 = 0 и a0 = 1, соответственно 0 + 0 = 0 и 1 + 0 = 1, как видим если первое слагаемое равно 0, то и на выходе 0, если первое слагаемое равно 1, то и на выходе 1, то есть сигнал повторяется, а соответственно нам становится не нужен логический элемент xor который в данном случае будет просто вносить задержку не выполняя никакой полезной функции, так же и со вторым логическим элементом в виду того, что p0 = 0. В результате оба логических элемента убираются, так как они просто повторители и сигнал a0 с входа сумматора просто подаётся на выход S0, то есть задержка появления результата в этом конкретном разряде составляет 0 нс, мгновенно получаем результат, жаль, что в остальных разрядах так не получится. В итоге мы проверили, что до этого, мы всё верно просчитали для 0-го бита нашего сумматора и его схема, до жути проста:

Далее, следует упомянуть о нахождении сигналов h0...h30, да именно до h30 так как после сложения в 32 разряде, бит переноса в старший разряд нам не нужен в виду того, что у нас сложение по модулю 32, а это ещё огромный кусок схемы отсекает, и не только в данном случае, но и во всех остальных. Эти сигналы, это сигналы распространения переноса и находятся они до жути просто, а в случае константы на одном из входов, то и ещё проще. Находятся они по формуле hi = ai or bi. Далее переходим к расчёту первого разряда, нулевой мы уже просчитали и вычислили. И да следует пояснить по поводу сигналов, их названий на схеме, как видим входной сигнал называется I0WI0 тут всегда в начале идёт обозначение номера итерации к которой относится сигнал I0 значит нулевая итерация, далее WI0 это входное слово Wi и цифра, это номер бита от 0 до 31. На выходе, опятьже I0 нулевая итерация, ADD3 это обозначение нашего сумматора Adder3 и OUT0, что это выходной сигнал и бит номер 0, думаю понятно...
Итак далее, наш сумматор для первого бита имеет ту же схему:
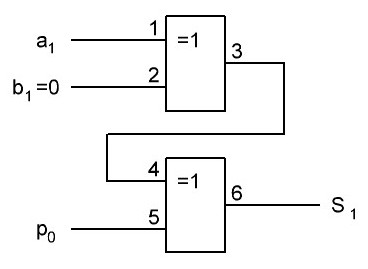
И мы уже видим, что из-за того, что b1=0, первый логический элемент опять превращается в повторитель, прямо магия какая-то превращается, превращается, а вот p0 мы сейчас рассмотрим ниже, для него мы имеем следующую формулу:
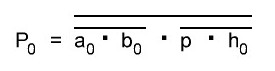
И как видим по сути это два логических элемента 2И-НЕ выходы которых подключены к ещё одному логическому элементу 2И-НЕ, это та общая черта обозначающая инверсию, которая над всей формулой, ладно, для большего понимания, начерчу схему данной формулы:
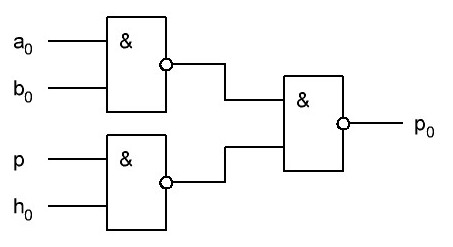
Тут у нас всё так же как и с элементом xor, только логика отличается, но суть такова, если на одном из входов логического элемента 2И-НЕ константа, то при константе равной лог. 0 на выходе будет всегда лог. 1, а если лог. 1 на одном из входов всегда, то это просто инвертор для второго сигнала. Итак, h0 у нас, это a0 xor b0 и нам известно, что b0=0, а при лог. 0 на одном из входов логического элемента ИЛИ даёт нам, что он становится повторителем для второго сигнала, выкидываем наш логический элемент ИЛИ из схемы и получаем
h0 = a0
В итоге движемся по схеме далее, верхний логический элемент 2 И-НЕ, на одном из входов b0=0, значит на его выходе будет постоянно лог. 1, которая поступает на один из выводов элемента 2 И-НЕ, среднем по схеме, на втором логическом элементе, нижнем по схеме у нас сигнал p присутствует, который всегда равен лог. 0, а соответственно на выходе будет всегда лог. 1. В итоге мы получаем, что на обоих входах, среднего по схеме, выходного логического элемента 2И-НЕ, присутствуют две константы всегда равные лог. 1, а значит на выходе всей этой схемы всегда будет присутствовать лог. 0 и соответственно p0 всегда равен лог. 0. Таким образом и второй логический элемент в нашем сумматоре, стал повторителем, а значит входной сигнал a1 опять проходит на выход, без какой либо задержки и схема, остаётся простой до жути:

Эхх, что-то хочется кушоц, пойду ка я приготовлю борщичёк... Но потом продолжу, обязательно продолжу...
Итак, пока там кипит... Находим h1. h1 = a1 or b1, b1= 0, а соответственно, элемент ИЛИ становится повторителем для сигнала a1, соответственно:
h1 = a1
Формула для вычисления, p1 с отброшенной последней частью будет:
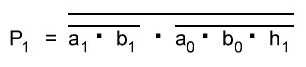
И что же мы тут видим, в первом выражении у нас b1 равен 0, а соответственно на выходе этого логического элемента всегда будет лог. 1, ну и на одном из входов последующего, во втором выражении b0 равен 0, а соответственно на выходе будет всегда лог. 1 и соответственно на выходе последнего логического элемента будет всегда лог. 0, то есть p1 будет всегда равен лог. 0 и это делает в схеме сумматора один из логических элементов повторителем, но и b2 у нас равен лог.0, что и второй логический элемент xor превращает в повторитель и таким образом наша схема продолжат быть до жути "сложной":

Ну вот, можно и приступать к просчёту 4-го разряда и схемы бита переноса для него, но позже, сейчас я заправлюсь борщичком по полной программе, скорее всего 2 раза, а пока буду это мероприятие производить, я ещё и сериал буду смотреть 3 сезон 12 серию "Помнить всё", а потом, продолжу, но, если не засну, но даже если и засну, до полуночи времени всё равно ещё много останется, так что обязательно сегодня продолжу, нужно сегодня обязательно расчитать, и вычертить, хотябы 8 разрядов сумматора...
Итак, пожрали, поспали, движемся дальше... Расчитываем и вычерчиваем сумматор третьего разряда и схему переноса для него. Изначальная схема у нас такая:
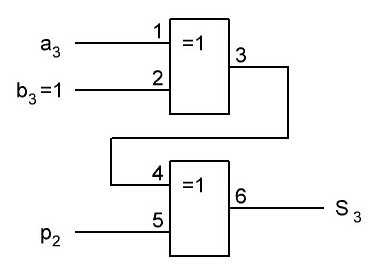
Так как b3 у нас равна лог. 1, то первый логический элемент становится инвертором для сигнала a3. Далее смотрим формулу для p2 и как видим во всех частях у нас присутствует константы b0, b1 и b2 которые равны 0, что приводит к тому, что на всех входах выходного элемента 3И-НЕ будут присутствовать лог. 1, а на выходе постоянно лог. 0, а соответственно и p2 будет всегда равен лог. 0
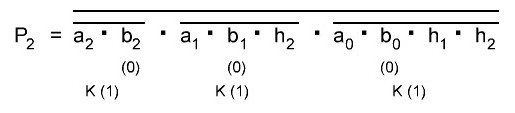
Таким образом, второй логический элемент xor в сумматоре становится повторителем и схема сумматора для этого разряда будет состоять только из одного инвертора и иметь минимально достижимую задержку 1 нс, а схема приобретает следующий вид:
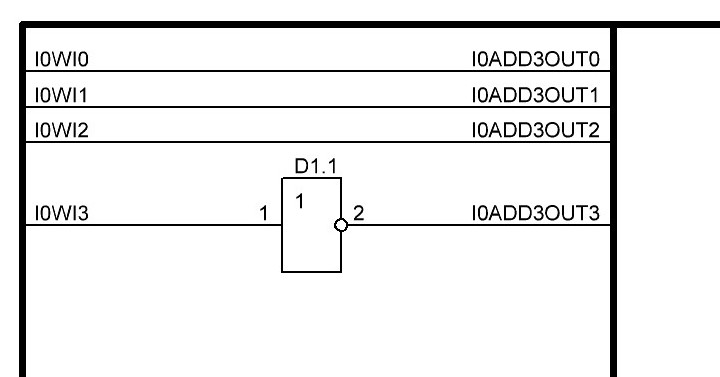
Далее переходим к расчёту четвёртого разряда сумматора и бита переноса p3 для него...
И как мы уже убедились, мы можем отбрасывать те части формулы, где есть хоть одна константа равная 0, таким образом формула для нахождения p3 будет иметь следующий вид:
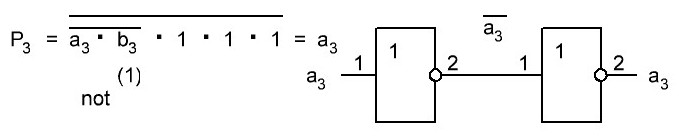
Как видим, из-за того, что b3 равна лог. 1 наш элемент становится инвертором и второй элемент, сначала становится элементом 2И-НЕ но и всё равно на втором выводе имеет констану единицу, поэтому так же становится инвертором, а включать два инвертора подрят нет смысла, только электроэнергию жечь, поэтому имеем p3 = a3. В самом же сумматоре b4 у нас равна лог. 0 и в результате имеем, схему сумматора состоящую из одного логического элемента xor на один вход которого подаётся 4-й разряд, а на второй перенос p3 который равен a3 и имеем следующую схему:
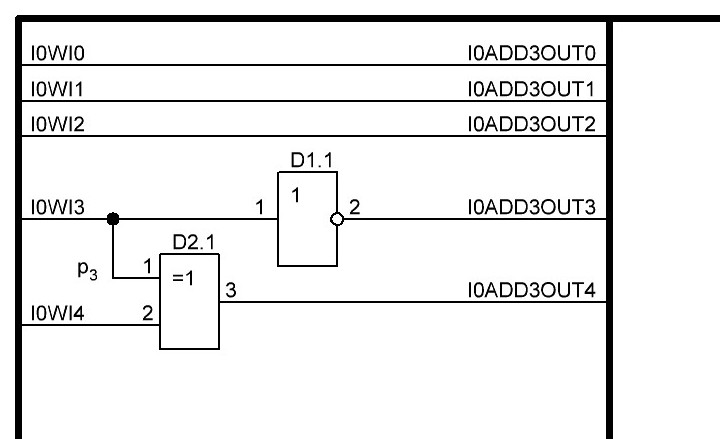
Переходим к пятому разряду... Для начала запишем:
h0 = a0
h1 = a1
h2 = a2
h3 = K (1)
h4 = a4
h5 = K (1)
h6 = K (1)
h7 = a7
h8 = K (1)
h9 = a9
h10 = K (1)
h11 = K (1)
Сумматор для 5-го разряда:
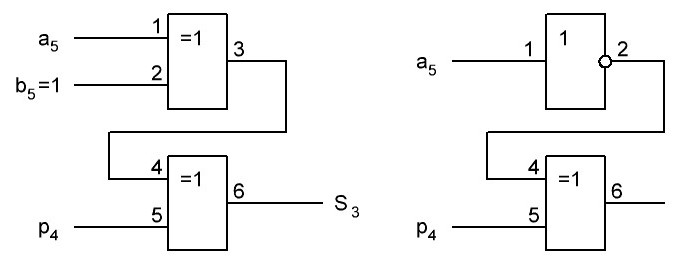
Формула:
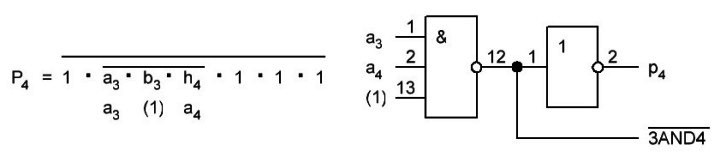
Тут можно было бы упростить просто до одного логического элемента 2И, но мы пока этого делать не будем, так как нам возможно в дальнейшем потребуется сигнал после /a3 and a4, а изменить схему позже, всегда можно. Так же применён логический элемент 3И-НЕ, а не 2И-НЕ, в силу того, что микросхема SN74AC00D имеет минимально достижимую задержку 1,5 нс, то есть больше на 0,5 нс, по сравнению с SN74AC10D, кажется немного, но учитывая большое количество итераций, набегает прилично, а нам нужно максимальное быстродействие. В результате имеем такую схему на данный момент:
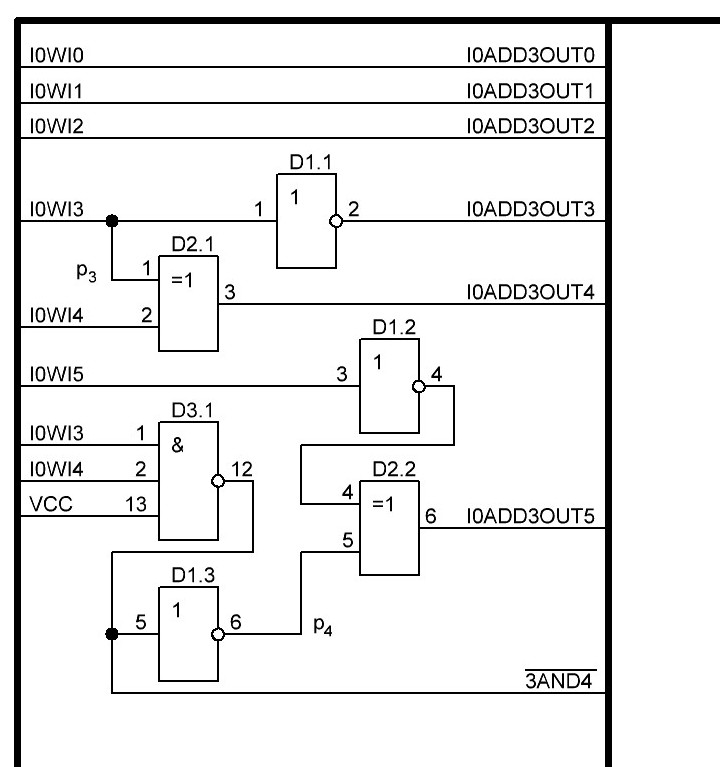
Нууу, на сегодня хватит, устал...
Новый день, продолжим, хоть и времени в обрез, нужно будет сходить денег на выходные заработать, чтобы спокойно позаниматься этим всем...
Итак 6-й разряд и бит переноса для него p5. Сигнал /3AND4 нам пригодился, как и выведеный на шину сигнал /I0WI5, на фото выше он ещё не выведен, но будет взят с элемента D1.2, так как нагрузочная способность уж точно не менее 10 у нас имеется в запасе, более точно нужно посмотреть в datasheet, но если честно не хочется перегружать микросхемы и в целях надёжности, да и для не снижения их быстродействия, поэтому будем условно считать, что у нас нагрузочная способность N=10. Итак формула и схема для p5:
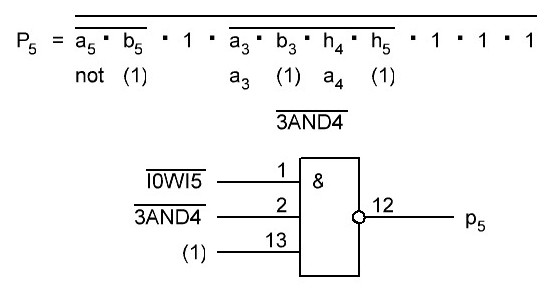
Так как b6 у нас равен лог.1, то a6 в сумматоре проходит на второй логический элемент через инвертор. И в результате имеем следующую схему на данный момент:
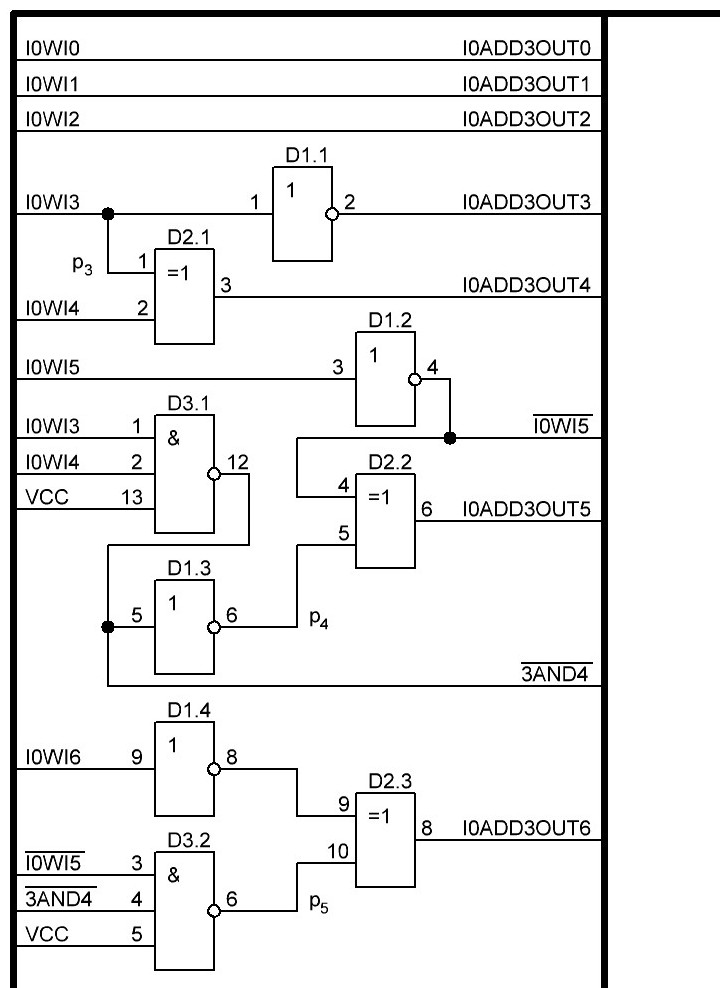
Далее седьмой разряд и бит переноса для него p6.
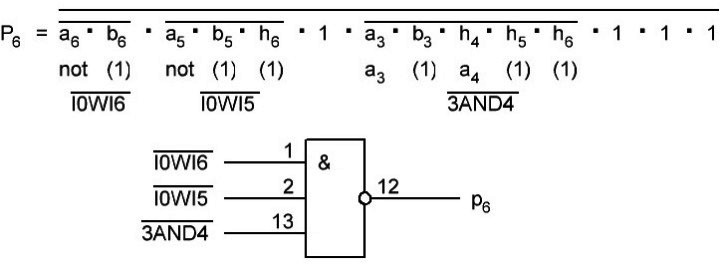
Так как b7 равен лог. 0, то первый логический элемент xor в сумматоре становится повторителем и опять попросту исключается, в итоге остаётся только второй логический элемент xor. И общая схема приобретает следующий вид:
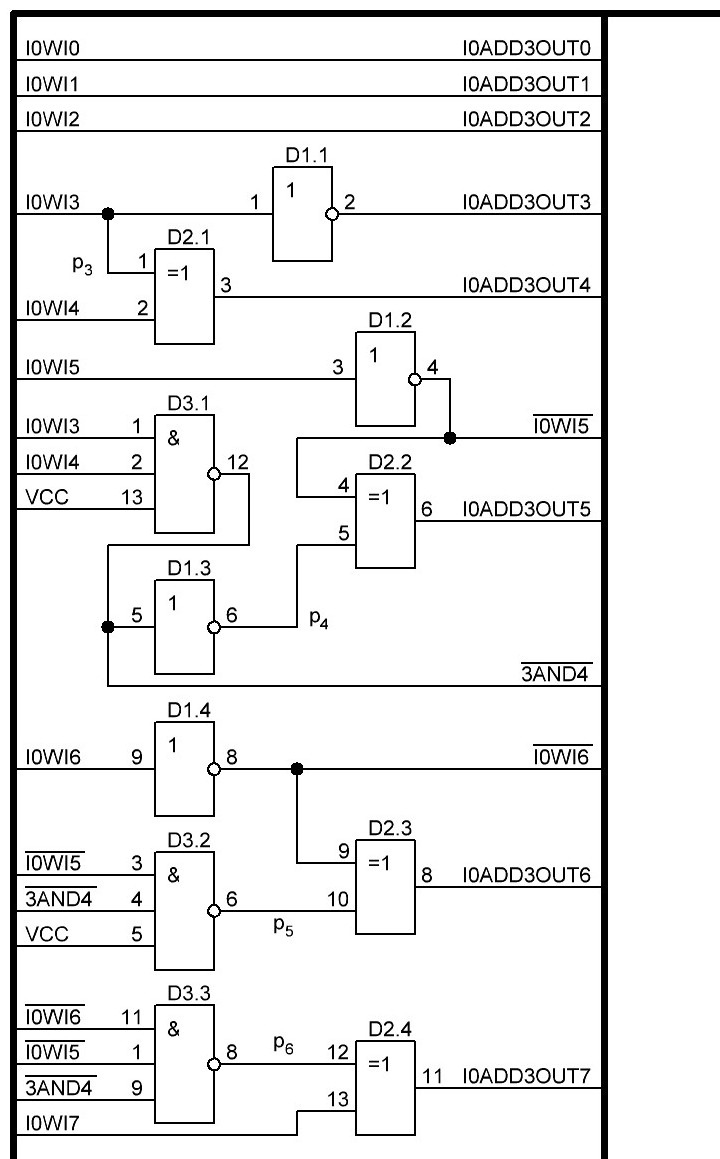
Нууу, вот и готовы первые 8 бит. Получилось вполне компактненько и экономично, всего 3 микросхемы и даже ещё свободна два инвертора, на плате это будет занимать, примерно 30 х 10 мм. Ладно пора собираться и бежать зарабатывать деревянные в оффлайне, в онлайне очередная, ежесуточная выплата капнула 4.83 NBX и хорошо, хотя тут нужно довести, чтобы 500 NBX капало в сутки и тогда можно будет спокойно заниматься электроникой и ни о чём не переживать. Дальнейшую разработку продолжу в следующем посте, впереди ещё 24 бита, но зато первые 8 уже проверил и перепроверил вдоль и поперёк, ладно, до новых встречь... хе-хе-хе, нужна мотивирующая картинка, чтобы дальше хорошо процесс шёл, для меня будет эта, мой лисёнок:

...
.
Поехали...
Итак, мы имеем сумматор, который имеет два 32-разрядных входа и один 32-разрядный выход. Первое слагаемое a, это переменная, а точнее слово w[0]. Второе слагаемое b, это константа с точно известным значением, а именно 0хF377ED68. А соответственно по сути у нас получается преобразователь данных, есть вход, на который подаётся переменная a и есть вход, на котором получается значение T1. Для начала запишем наше число в двоичной форме, пожалуй это будет лучше сделать в графическом виде, я для этого использую программу Splan в которой я черчу схемы и вообще всё, что угодно, так как более простой в освоении программы, мне потребовался 1 час, чтобы разобраться в ней, и удобной в использовании, я ещё не встречал. Ну а потом просто конвертирую в .bmp формат, для этого в ней имеется кнопочка, пойду почерчу...
Готово, загрузим, а нет не загрузим, у нас как всегда ipic.su не доступен Error 521 Web server is down, как же это за..бало, но мы пойдём другим путём...

Все нервы измотали, но как вроде нашёл, куда грузится и работает vfl.ru
Итак, хух, на рисунке выше наше входное слово b, теперь оно представлено наглядно и всегда можно посмотреть какой бит чему равен. Для нас максимально выгодно, чтобы в нём, да и в любом другом было как можно больше нулей, это кардинально сокращает количество "железа", но что имеем, то имеем, с этим и будем работать. Так же нам здесь очень везёт, что входной бит переноса из младшего разряда p не используется и по сути всегда равен нулю, это вообще отрезает огромный кусок схемы и не только тут, но и в дальнейшем, где оба слагаемых будут переменными. Далее представим нашу формулу, опять чертить...

Как видим в последней части формулы у нас присутствует бит переноса из младшего разряда p, а он у нас всегда равен нулю, соответственно присутствуя на входе логического элемента И-НЕ он создаёт условие, что у нас на выходе этого логического элемента всегда будет лог. 1 и таким образом, нет смысла реализовывать данный логический элемент в "железе", достаточно просто подать лог. 1 на вход следующего элемента И-НЕ, но и это не нужно делать, так как лог. 1 на многовходовом логическом элементе И-НЕ, если она константа и всегда равна лог. 1, просто убирает данный вход. Например, если у нас логический элемент 4И-НЕ и на один из входов постоянно подаётся лог. 1, то он просто превращается в логический элемент 3И-НЕ. Таким образом последняя часть формулы отпадает во всех случаях, вне зависимости от того, обе переменные у нас на входе сумматора или одна из них равна константе, так как входной бит переноса из младшего разряда у нас всегда равен лог.0. Далее перейдём к реализации, а точнее проверки 0-го бита нашего сумматора. Итак, мы имеем вход a значение которого мы не знаем и вход b значение которого мы знаем. Так как мы расчитываем 0-й бит, то и входные слагаемые у нас a0 и b0, входной бит переноса равен нулю. Для этого нам нужно вычертить схему одного разряда сумматора, и она будет идентичная для всех разрядов, и самое главное, что в ней нам не требуется реализовывать выходной бит переноса, так как у нас параллельный сумматор с параллельным переносом, пойду почерчу, не я конечно пойду кофе пить и курить, а потом...

Вот и наш сумматор, схема в данном случае универсальная, для всех разрядов, то есть, если бы у нас на обоих входах были переменные, а так и будет в последующих итерациях, то для 32 разрядов требуется 16 микросхем SN74AC86D которая содержит 4 логических элемента "исключающее ИЛИ" (xor), по два логических элемента на один разряд. Но в данном конкретном нулевом разряде у нас p=0, также b0=0. И тут у нас получается хорошая возможность сократить количество "железа", так как известно, что если на одном из входов логического элемента "исключающее ИЛИ" присутствует константа лог. 1, то элемент становится инвертором, а если лог. 0, то повторителем. Это легко проверить по таблице истиности или по самому свойству данного логического элемента, так как это сумматор, но без бита переноса в старший разряд:
0 + 0 = 0; 0 + 1 = 1; 1 + 0 = 1; 1 + 1 =0 В последнем случае еденица переходит в старший разряд, но так как у элемента xor она отбрасывается, то и получается 1 + 1 = 0.
Теперь как видим если у нас b0=0, то есть будет два возможных варианта a0 = 0 и a0 = 1, соответственно 0 + 0 = 0 и 1 + 0 = 1, как видим если первое слагаемое равно 0, то и на выходе 0, если первое слагаемое равно 1, то и на выходе 1, то есть сигнал повторяется, а соответственно нам становится не нужен логический элемент xor который в данном случае будет просто вносить задержку не выполняя никакой полезной функции, так же и со вторым логическим элементом в виду того, что p0 = 0. В результате оба логических элемента убираются, так как они просто повторители и сигнал a0 с входа сумматора просто подаётся на выход S0, то есть задержка появления результата в этом конкретном разряде составляет 0 нс, мгновенно получаем результат, жаль, что в остальных разрядах так не получится. В итоге мы проверили, что до этого, мы всё верно просчитали для 0-го бита нашего сумматора и его схема, до жути проста:

Далее, следует упомянуть о нахождении сигналов h0...h30, да именно до h30 так как после сложения в 32 разряде, бит переноса в старший разряд нам не нужен в виду того, что у нас сложение по модулю 32, а это ещё огромный кусок схемы отсекает, и не только в данном случае, но и во всех остальных. Эти сигналы, это сигналы распространения переноса и находятся они до жути просто, а в случае константы на одном из входов, то и ещё проще. Находятся они по формуле hi = ai or bi. Далее переходим к расчёту первого разряда, нулевой мы уже просчитали и вычислили. И да следует пояснить по поводу сигналов, их названий на схеме, как видим входной сигнал называется I0WI0 тут всегда в начале идёт обозначение номера итерации к которой относится сигнал I0 значит нулевая итерация, далее WI0 это входное слово Wi и цифра, это номер бита от 0 до 31. На выходе, опятьже I0 нулевая итерация, ADD3 это обозначение нашего сумматора Adder3 и OUT0, что это выходной сигнал и бит номер 0, думаю понятно...
Итак далее, наш сумматор для первого бита имеет ту же схему:

И мы уже видим, что из-за того, что b1=0, первый логический элемент опять превращается в повторитель, прямо магия какая-то превращается, превращается, а вот p0 мы сейчас рассмотрим ниже, для него мы имеем следующую формулу:
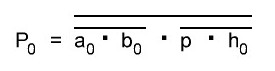
И как видим по сути это два логических элемента 2И-НЕ выходы которых подключены к ещё одному логическому элементу 2И-НЕ, это та общая черта обозначающая инверсию, которая над всей формулой, ладно, для большего понимания, начерчу схему данной формулы:

Тут у нас всё так же как и с элементом xor, только логика отличается, но суть такова, если на одном из входов логического элемента 2И-НЕ константа, то при константе равной лог. 0 на выходе будет всегда лог. 1, а если лог. 1 на одном из входов всегда, то это просто инвертор для второго сигнала. Итак, h0 у нас, это a0 xor b0 и нам известно, что b0=0, а при лог. 0 на одном из входов логического элемента ИЛИ даёт нам, что он становится повторителем для второго сигнала, выкидываем наш логический элемент ИЛИ из схемы и получаем
h0 = a0
В итоге движемся по схеме далее, верхний логический элемент 2 И-НЕ, на одном из входов b0=0, значит на его выходе будет постоянно лог. 1, которая поступает на один из выводов элемента 2 И-НЕ, среднем по схеме, на втором логическом элементе, нижнем по схеме у нас сигнал p присутствует, который всегда равен лог. 0, а соответственно на выходе будет всегда лог. 1. В итоге мы получаем, что на обоих входах, среднего по схеме, выходного логического элемента 2И-НЕ, присутствуют две константы всегда равные лог. 1, а значит на выходе всей этой схемы всегда будет присутствовать лог. 0 и соответственно p0 всегда равен лог. 0. Таким образом и второй логический элемент в нашем сумматоре, стал повторителем, а значит входной сигнал a1 опять проходит на выход, без какой либо задержки и схема, остаётся простой до жути:

Эхх, что-то хочется кушоц, пойду ка я приготовлю борщичёк... Но потом продолжу, обязательно продолжу...
Итак, пока там кипит... Находим h1. h1 = a1 or b1, b1= 0, а соответственно, элемент ИЛИ становится повторителем для сигнала a1, соответственно:
h1 = a1
Формула для вычисления, p1 с отброшенной последней частью будет:
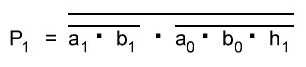
И что же мы тут видим, в первом выражении у нас b1 равен 0, а соответственно на выходе этого логического элемента всегда будет лог. 1, ну и на одном из входов последующего, во втором выражении b0 равен 0, а соответственно на выходе будет всегда лог. 1 и соответственно на выходе последнего логического элемента будет всегда лог. 0, то есть p1 будет всегда равен лог. 0 и это делает в схеме сумматора один из логических элементов повторителем, но и b2 у нас равен лог.0, что и второй логический элемент xor превращает в повторитель и таким образом наша схема продолжат быть до жути "сложной":

Ну вот, можно и приступать к просчёту 4-го разряда и схемы бита переноса для него, но позже, сейчас я заправлюсь борщичком по полной программе, скорее всего 2 раза, а пока буду это мероприятие производить, я ещё и сериал буду смотреть 3 сезон 12 серию "Помнить всё", а потом, продолжу, но, если не засну, но даже если и засну, до полуночи времени всё равно ещё много останется, так что обязательно сегодня продолжу, нужно сегодня обязательно расчитать, и вычертить, хотябы 8 разрядов сумматора...
Итак, пожрали, поспали, движемся дальше... Расчитываем и вычерчиваем сумматор третьего разряда и схему переноса для него. Изначальная схема у нас такая:

Так как b3 у нас равна лог. 1, то первый логический элемент становится инвертором для сигнала a3. Далее смотрим формулу для p2 и как видим во всех частях у нас присутствует константы b0, b1 и b2 которые равны 0, что приводит к тому, что на всех входах выходного элемента 3И-НЕ будут присутствовать лог. 1, а на выходе постоянно лог. 0, а соответственно и p2 будет всегда равен лог. 0
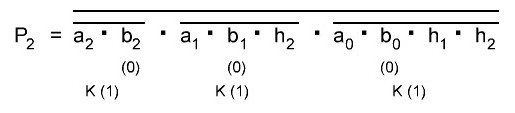
Таким образом, второй логический элемент xor в сумматоре становится повторителем и схема сумматора для этого разряда будет состоять только из одного инвертора и иметь минимально достижимую задержку 1 нс, а схема приобретает следующий вид:

Далее переходим к расчёту четвёртого разряда сумматора и бита переноса p3 для него...
И как мы уже убедились, мы можем отбрасывать те части формулы, где есть хоть одна константа равная 0, таким образом формула для нахождения p3 будет иметь следующий вид:
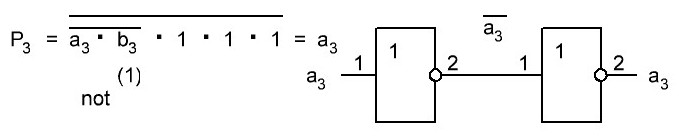
Как видим, из-за того, что b3 равна лог. 1 наш элемент становится инвертором и второй элемент, сначала становится элементом 2И-НЕ но и всё равно на втором выводе имеет констану единицу, поэтому так же становится инвертором, а включать два инвертора подрят нет смысла, только электроэнергию жечь, поэтому имеем p3 = a3. В самом же сумматоре b4 у нас равна лог. 0 и в результате имеем, схему сумматора состоящую из одного логического элемента xor на один вход которого подаётся 4-й разряд, а на второй перенос p3 который равен a3 и имеем следующую схему:

Переходим к пятому разряду... Для начала запишем:
h0 = a0
h1 = a1
h2 = a2
h3 = K (1)
h4 = a4
h5 = K (1)
h6 = K (1)
h7 = a7
h8 = K (1)
h9 = a9
h10 = K (1)
h11 = K (1)
Сумматор для 5-го разряда:

Формула:
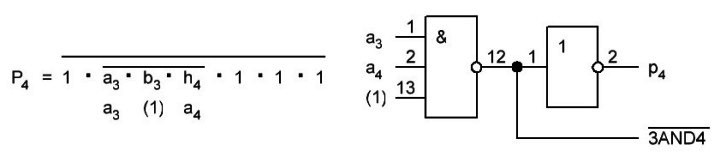
Тут можно было бы упростить просто до одного логического элемента 2И, но мы пока этого делать не будем, так как нам возможно в дальнейшем потребуется сигнал после /a3 and a4, а изменить схему позже, всегда можно. Так же применён логический элемент 3И-НЕ, а не 2И-НЕ, в силу того, что микросхема SN74AC00D имеет минимально достижимую задержку 1,5 нс, то есть больше на 0,5 нс, по сравнению с SN74AC10D, кажется немного, но учитывая большое количество итераций, набегает прилично, а нам нужно максимальное быстродействие. В результате имеем такую схему на данный момент:

Нууу, на сегодня хватит, устал...
Новый день, продолжим, хоть и времени в обрез, нужно будет сходить денег на выходные заработать, чтобы спокойно позаниматься этим всем...
Итак 6-й разряд и бит переноса для него p5. Сигнал /3AND4 нам пригодился, как и выведеный на шину сигнал /I0WI5, на фото выше он ещё не выведен, но будет взят с элемента D1.2, так как нагрузочная способность уж точно не менее 10 у нас имеется в запасе, более точно нужно посмотреть в datasheet, но если честно не хочется перегружать микросхемы и в целях надёжности, да и для не снижения их быстродействия, поэтому будем условно считать, что у нас нагрузочная способность N=10. Итак формула и схема для p5:

Так как b6 у нас равен лог.1, то a6 в сумматоре проходит на второй логический элемент через инвертор. И в результате имеем следующую схему на данный момент:

Далее седьмой разряд и бит переноса для него p6.

Так как b7 равен лог. 0, то первый логический элемент xor в сумматоре становится повторителем и опять попросту исключается, в итоге остаётся только второй логический элемент xor. И общая схема приобретает следующий вид:

Нууу, вот и готовы первые 8 бит. Получилось вполне компактненько и экономично, всего 3 микросхемы и даже ещё свободна два инвертора, на плате это будет занимать, примерно 30 х 10 мм. Ладно пора собираться и бежать зарабатывать деревянные в оффлайне, в онлайне очередная, ежесуточная выплата капнула 4.83 NBX и хорошо, хотя тут нужно довести, чтобы 500 NBX капало в сутки и тогда можно будет спокойно заниматься электроникой и ни о чём не переживать. Дальнейшую разработку продолжу в следующем посте, впереди ещё 24 бита, но зато первые 8 уже проверил и перепроверил вдоль и поперёк, ладно, до новых встречь... хе-хе-хе, нужна мотивирующая картинка, чтобы дальше хорошо процесс шёл, для меня будет эта, мой лисёнок:

...
.
Последний раз редактировалось: Viktor2312 (Чт Июн 25 2020, 09:37), всего редактировалось 40 раз(а)
Viktor2312- RIP
- Сообщения : 15492
Дата регистрации : 2012-08-10
Возраст : 45
Откуда : Пятигорск
 .
.
8
.
В общим попробовал сложить с числом 0х21 ради эксперимента, числа могут быть в нашем случае от 0х00 до 0xFF, взял вот из начала число 68 + 21 = 89, проверил в виндовом и обычном калькуляторе, надо же и правда 89 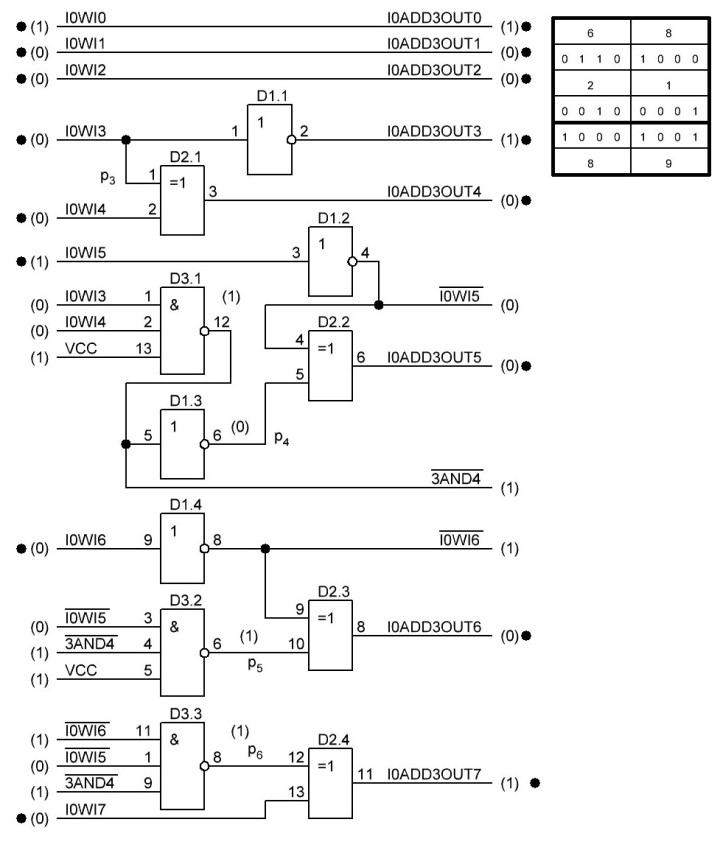
Проверил с числом 0х8A, результат получился верным:
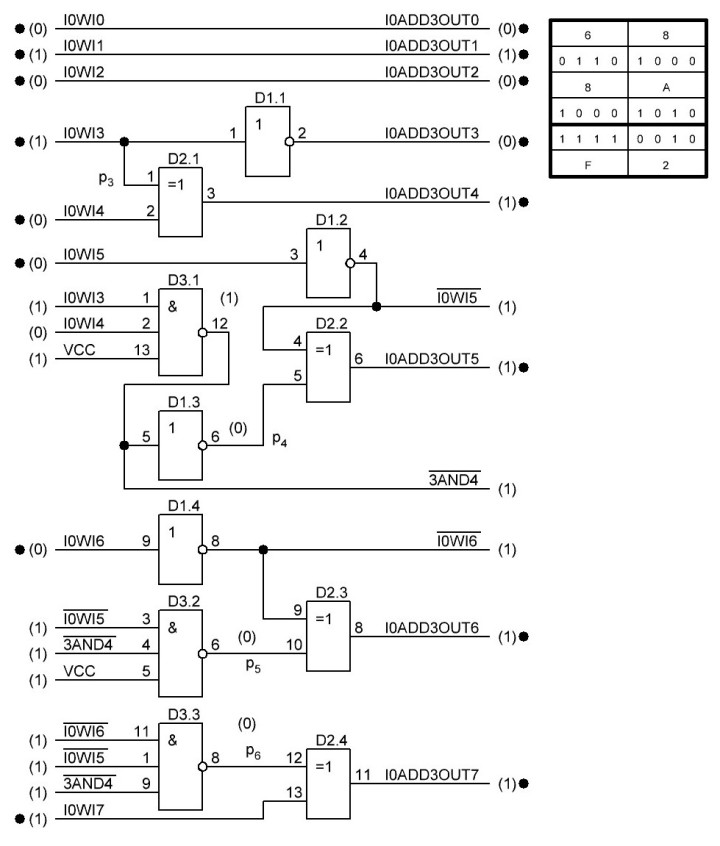
В общим, решил я всё же, что тут можно применить логические элементы 2И-НЕ микросхема SN74AC00D, хоть они и имеют минимально достижимую задержку 1,5 нс, так как это младшие разряды и задержки тут всё равно минимальны. А по мере продвижения к более старшим разрядам они неминуемо вырастут из-за того, что потребуются логические элементы с большим числом входов и их придётся создавать из элементов с меньшим количеством входов, а соответственно будет как минимум 2 кванта времени по 1 нс, и как следствие общая задержка составного элемента будет 2 нс, а общая как минимум 4 нс. Так как, всё равно минимальное время получения верного результата на всех битах, будет равно времени, которое имеет та схема бита переноса, которая имеет максимальную задержку и плюс задержка в сумматоре в 1 нс.
Ниже формула для бита переноса p7 и схема, а также схема сумматора для a8
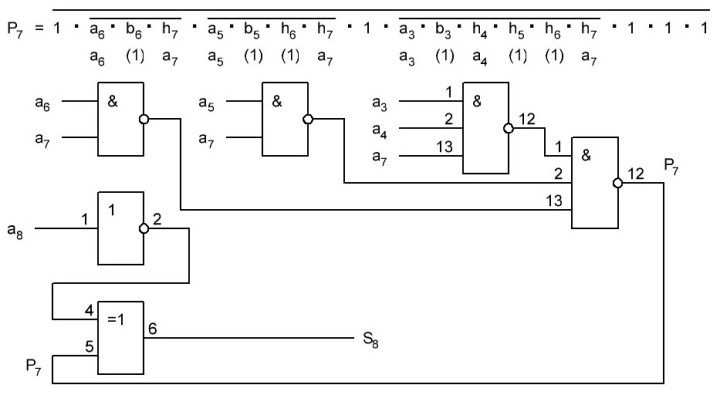
Естественно схему пришлось изменить, заменив логические элементы 3И-НЕ на 2И-НЕ. И на данный момент имеем задействованными 5 микросхем, но есть ещё один свободный элемент НЕ и три элемента "исключающее ИЛИ".
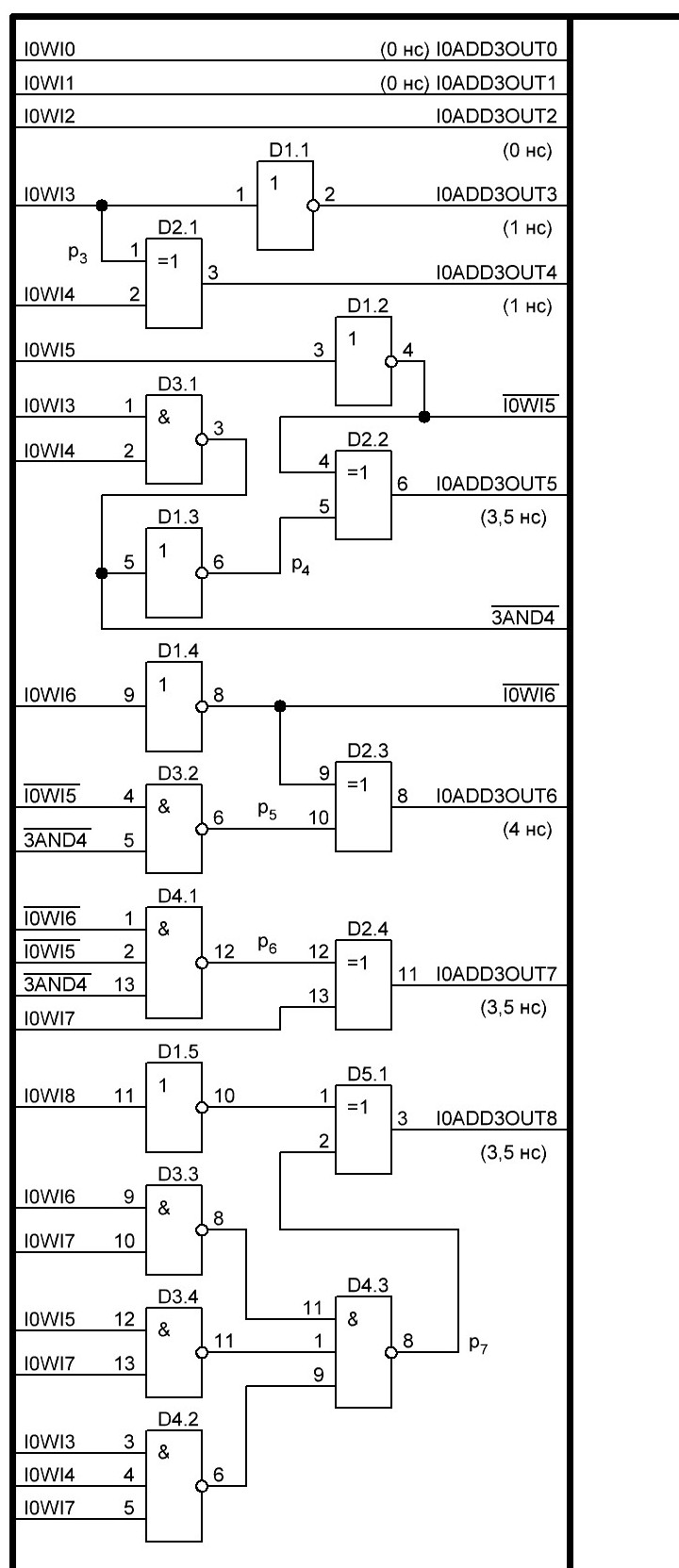
Проверил схему с числом 0хA9, такое число, чтобы бит p7 по логике был равен лог. 1 в итоге 68 + A9 = 111. Результат совпал, можно двигаться дальше:
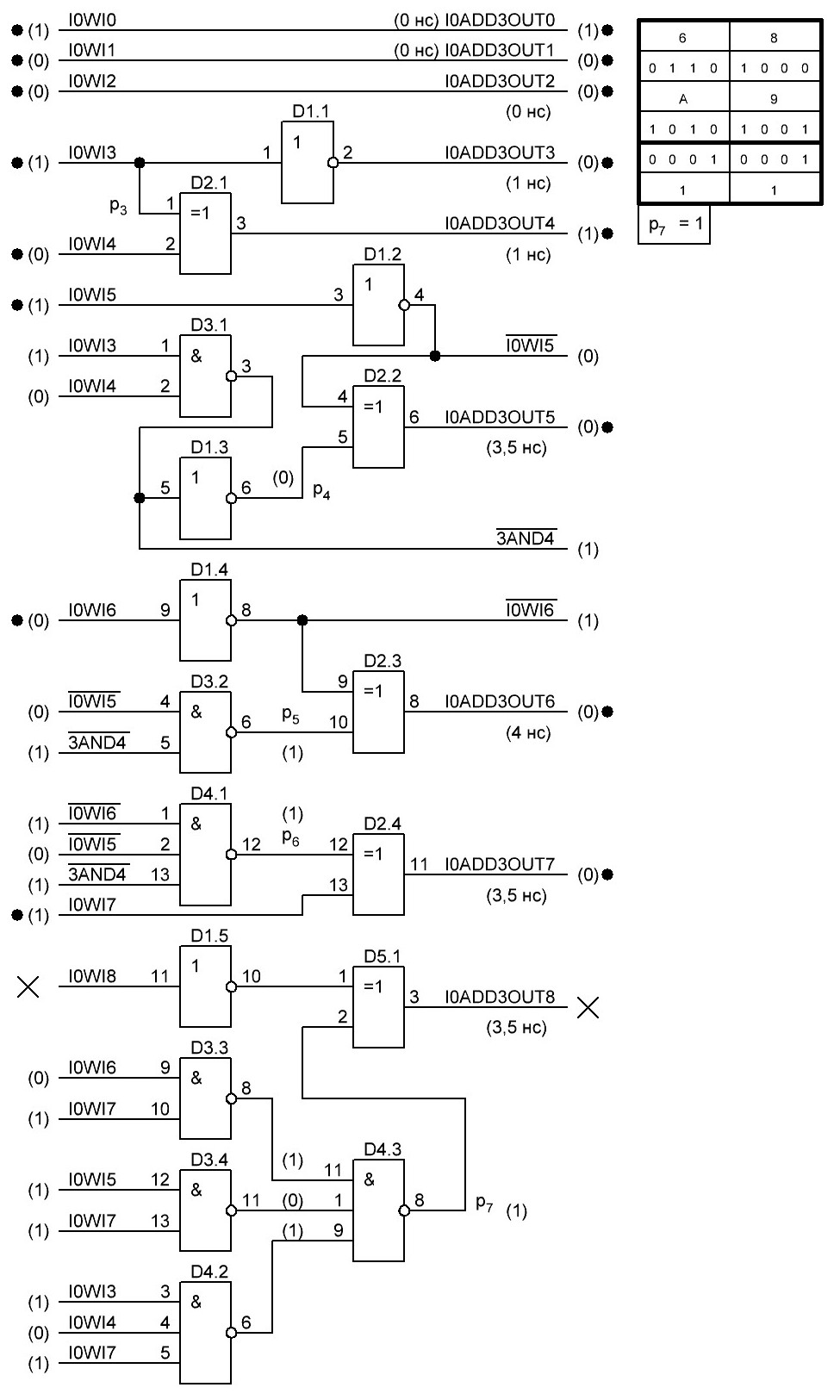
...
.
Последний раз редактировалось: Viktor2312 (Вт Июн 23 2020, 07:44), всего редактировалось 7 раз(а)
Viktor2312- RIP
- Сообщения : 15492
Дата регистрации : 2012-08-10
Возраст : 45
Откуда : Пятигорск
 .
.
9
.
Далее, расчитываем p8 и S9 ниже формула и схема: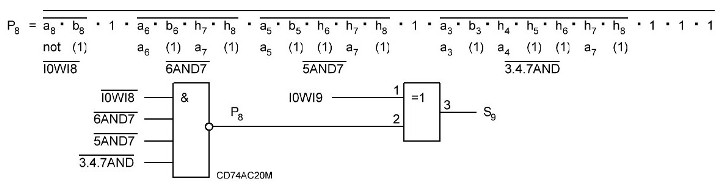
И основная схема с внесёнными изменениями:
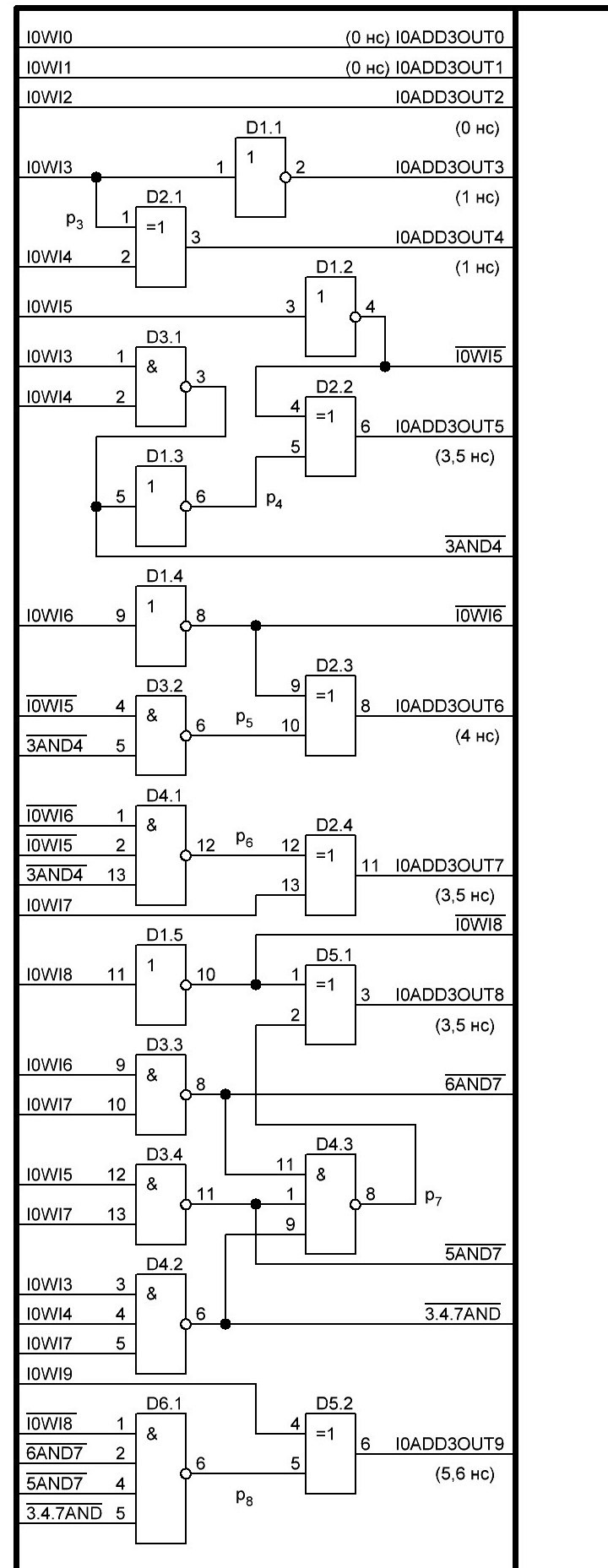
Далее, расчитываем p9 и S10 ниже формула и схема:
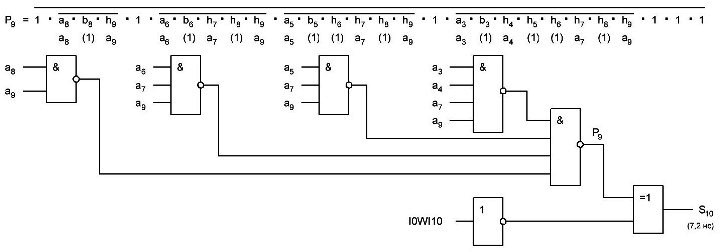
Как видим задержка уже стала очень большой 7,2 нс, её можно уменьшить применив вместо 4И-НЕ элементов составные элементы, что даст задержку в 2 нс на каждом и общая задержка будет 5 нс, вместо 7,2 нс, но и это много, к тому же у нас сильная нагрузка по входам получается.
Тут напрашивается вывод, что нужно делать комбинированную схему, применяя готовые сумматоры на 4 разряда начиная с 4 бита. Первые 4 бита у нас можно реализовать без микросхемы сумматора, только на одном инверторе, и получением бита переноса p3 мгновенно. То есть биты a0...a3 и бит переноса реализуются на одной микросхеме и остаётся свободно 5 инверторов, которые можно применить далее. Следующие 4 бита. сложение реализовать на готовом 4-х разрядном сумматоре, а бит переноса p7 получать отдельно, на логике, так как на логике выходит задержка 2 нс, а с микросхемы он выходит через 2,7 нс. Далее нужно просчитать за какое время мы сможем получить бит переноса p11 и если время его получения будет меньше 2,7 нс, то так же реализовать схему его получения на логике, если дольше, то остальная вся часть сумматора будет строиться на готовых микросхемах. Если бы мы всю схему реализовали на 8 микросхемах сумматоров, то наша задержка составила бы 2,7 *7 +3,3 = 22,2 нс, но так как первой микросхемы не будет, а вместо неё только один инвертор и мгновенное получение бита переноса, то имеем 2,7 *6 + 3,3 = 19,5 нс, при получении бита переноса p7 отдельно на логике имеем задержку 2 нс, и времы ещё уменьшается на 0,7 нс, в итоге имеем: 2+ 2,7 *5 + 3,3 = 18,8 нс. Теперь нужно просчитать p11, чтобы точно уже знать, как дальше реализовывать схему и получится ли у нас иметь минимально достижимое время нашего сумматора Adder3 меньше 18,8 нс.
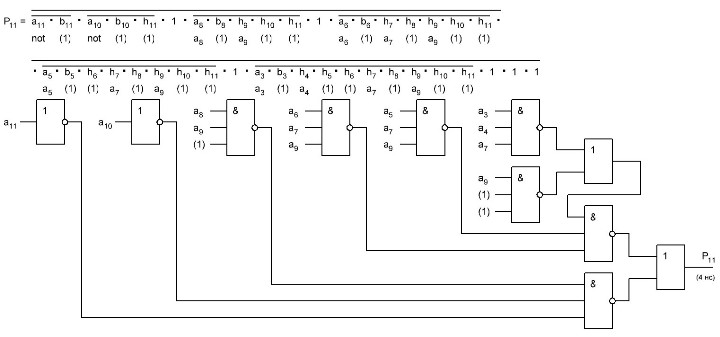
Как видно из формулы и схемы выше, бит переноса p11 у нас получается дольше чем за 2,7 нс, за 4 нс. Значит брать мы его уже будем непосредственно с микросхемы сумматора. И таким образом у нас получается, что будет применено 7 микросхем сумматора и логика для получения бита p7 за 2 нс. И максимально достижимое быстродействие нашего сумматора будет 18,8 нс.
Осталось выделить время и начертить окончательную схему...
.
Последний раз редактировалось: Viktor2312 (Чт Июн 25 2020, 11:34), всего редактировалось 13 раз(а)
Viktor2312- RIP
- Сообщения : 15492
Дата регистрации : 2012-08-10
Возраст : 45
Откуда : Пятигорск
 .
.
10
.
Вот собственно и готов сумматор Adder3. Вышло 10 микросхем в общей сложности, но остались свободными 5 логических элементов НЕ и 2 логических элемента 3И-НЕ, которые можно будет задействовать впоследствии. Так же 1 резистор и на схеме пока не показаны, но будет ещё 10 блокировочных конденсатором по 0,1 мкФ. На плате, это займёт примерно 100 х 15 мм, возможно меньше, это так, прикидки на глаз.Схема:

Теперь можно приступать к разработке следующего сумматора Adder5.
.
Последний раз редактировалось: Viktor2312 (Чт Июн 25 2020, 17:27), всего редактировалось 5 раз(а)
Viktor2312- RIP
- Сообщения : 15492
Дата регистрации : 2012-08-10
Возраст : 45
Откуда : Пятигорск
 .
.
11
.
Движемся дальше, в Adder5 будем применять 8 микросхем сумматоров, но для второй микросхемы уже точно будем использовать бит переноса p3 построенный отдельно, а не с самой микросхемы, это нам даст выигрыш в 0,7 нс и для схемы получения его, у нас как раз есть свободные, оставшиеся логические элементы: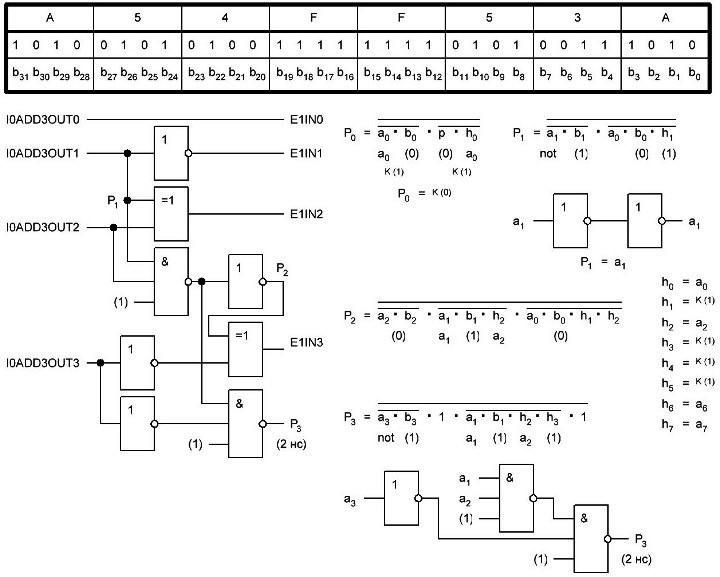
Теперь нужно разработать схему для бита переноса p7 и посмотреть какая выйдет задержка и сколько потребуется логических элементов...
А логических элементов потребуется много, как выяснилось, либо 3 микросхемы с элементами 3И-НЕ и задержка выходит 4 нс, если брать с микросхемы, то корректный бит переноса будет у нас через 2 + 2,7 нс, то есть через 4,7 нс. Это нас утраивает и соответственно отпадает необходимость формировать отдельно бит переноса p3, так как не важно через 2 или 2,7 нс он будет корректным, важным будет время формирования бита переноса p7, он задаёт нам задержку в 4 нс появления бита переноса после первых двух микросхем. Затем будет 5 задержек по 2,7 нс и на последней 3,3 нс, итого выходит, максимально достижимое быстродействие сумматора Adder5 равным: 4 + 2,7 * 5 + 3,3 нс = 20,8 нс. И таким образо выходит, что переменная E для второй итерации будет сформирована через 39,6 нс после подачи слова w[0]. Естественно напомню, что это максимально короткое время, которое можно достичь, учитывая параметры из datasheet и при соблюдении многих условий, таких как питание +5,5 В, кристалл микросхемы должен быть с диапазоном до +125 оС, проводники на плате иметь минимальную длину, не должно быть прямых углов у дорожек, дорожки на разных сторонах платы должны проходить не горизонтально, а под углом 90о и т. д. и т. п. Там ещё очень много условий, которые кстати все придётся соблюсти:
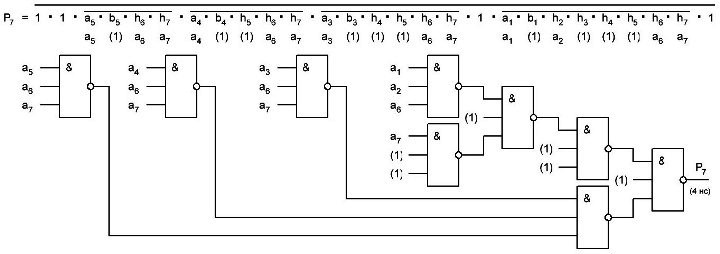
Теперь можно приступать к черчению схемы, она получается довольно простой и однообразной. Задействовано будет 3 отдельные микросхемы SN74AC10D, а оставшиеся от сумматора Adder3 пока будут не задействованы, и таким образом выходит, что сумматор Adder5 будет построен на 11 микросхемах...
А хотя нет, немножечько накосяпорил, при составном элементе, нам же нужен элемент 2ИЛИ, а не И-НЕ, вот отвлёкся чуток, и чуть ошибку не сделал, но мы это сейчас поправим, и количество микросхем всё равно не меняется 11 шт. на сумматор, а вот свободных элементов немного прибавится...
И схема, на данный момент, на ней Adder3 и Adder5 реализованы:
Итак, у нас вышло, что I0Adder3 имеет быстродействие 18,8 нс. Именно через такое время будут получены старшие 4 разряда, всё бы замечательно, но, нам нужно быстродействие. Поэтому нужно ещё ускорить его. Для этого придётся увеличить объём "железа". Какая у нас основная проблема, это бит переноса, мы его ждём из предыдущего разряда и не можем двигаться дальше, а параллельный перенос полноценный, мы не можем реализовать из-за отсутствия многовходовых логических элементов. А построение составных логических элементов с большим количеством входов из элементов с меньшим количеством входов, опять же дают нам задержки больше, чем выдаёт готовый 4-х разрядный сумматор SN74ACT283M, выполненный в виде одной микросхемы, напомню мы имеет выход результата через 3,3 нс, а бита переноса через 2,7 нс. Но, есть маленькая хитрость, если, например мы имеем включённые два сумматора с последовательным битом переноса между тетрадами и соответственно получением бита переноса через 2,7 + 2,7 = 5,4 нс, то мы можем принять время подачи данных за t0, именно с этого момента у нас начнутся все вычисления и соответственно через 5,4 нс изменится значение бита переноса в старшие разряды, но как быть, ведь у нас ещё не готов и неизвестно правильное значение входного бита переноса из младших разрядов. И вот тут, мы можем применить две идентичные схемы, но на первой входной бит переноса подсоединён к лог. 0, а на второй к лог. 1 и тем самым мы имеем два значения, как данных, так и выходного бита переноса в старшие разряды. И нам остаётся только при помощи двух мультиплексоров 4хMX2-1 выбрать правильные данные и при помощи ещё одной микросхемы, в которой 3 мультиплексора будут незадействованы, выбрать правильный бит переноса в старшие разряды. Тут тоже всё не так просто, так как сама микросхема мультиплексора имеет задержку на выбор входа, который будет соединён с выходом, а именно 1,5 нс. И потом сами данные с входа на выход проходят с задержкой 2,1 нс. Это приходится учитывать и выигрыш в времени получается начиная с 9 бита числа и далее. В общим осталось просчитать задержки, добиться максимального быстродействия, хотя пока выигрыш точно можно получить в 1,9 нс, дальше не просчитывал, но думаю больше, и вычертить схему, и тогда можно будет приступать к разработке печатной платы, в виде небольшого модуля у которого будет 32 контакта вход, на который подаётся число W[0] и выход 32 контакта T2, и естественно по несколько контактов для подачи напряжения питания. Небольшие модули позволят во первых под ними на основной плате располагать другие микросхемы, ну и в случае применения другой элементной базы, заменять модули, правда при помощи выкусывания этих контактов, так как разъёмы получаются слишком громоздкими. А так можно использовать либо тонкий лужёный провод, либо обрезки от выводов резисторов и расположить их с очень мелким шагом, а по углам, крепить плату при помощи более толстых 4-х контактов, соединённых с общим прободом, но это всё не точно, просто прикидки на будущее...
.
Последний раз редактировалось: Viktor2312 (Пн Июл 27 2020, 22:53), всего редактировалось 10 раз(а)
Viktor2312- RIP
- Сообщения : 15492
Дата регистрации : 2012-08-10
Возраст : 45
Откуда : Пятигорск
 .
.
12
.
____Итак, что мы имеем, после просчёта задержек распространения сигнала, вышло, что есть смысл применить условный сумматор в 5, 6 и 7 тетрадах. Хотя условным его сложно назвать, так как внутри каждой микросхемы находится параллельный сумматор с параллельным переносом, внешне именно в этих тетрадах реализован условный сумматор, ну а между частью тетрад реализован последовательный перенос. Поэтому правльно будет назвать, что у нас получился комбинированный сумматор.
____Изначально планировалось применение мультиплексоров КП16, а именно их импортных аналогов в серии 74AC (CD74AC157M), у которого время выбора входа 1,5 нс, а время прохождения данных с входа на выход 2,1 нс. Но так как по быстродействию больший эффект даёт уменьшение времени выбора входа, то решено было посмотреть на КП11, а именно CD74AC257M, у неё время выбора входа 1,1 нс, а время прохождения данных с входа на выход 2,3 нс. Конечно же, если бы этих зедержек не было бы, то всё было бы просто супер классно, но к сожалению мы живём в реальном мире, а не в идеальном, где существуют идеальные параметры...
____В результате, минимальное время получения результата в последней, восьмой тетраде, которое мы можем получить на модернизированном сумматоре, естественно при условии, идеального монтажа, соблюдения всех рекомендаций из datasheet для получения минимального времени распространения сигнала и при очень качественных образцах самих микросхем, это 14,1 нс. То есть по сравнению с предыдущей версией нашего сумматора, которая имела этот параметр равным 18,8 нс, мы получили выигрыш в 4,7 нс. Но и количество микросхем возросло с 10 до 16, что я считаю приемлемым. В результате имеем предварительно-окончательную схему сумматора I0Adder3. Так же было решено дать название, прибору, устройству, да не суть важно. "Асинхронный Hard майнер биткоина" или по английски, но в виде аббревиатуры "AHMB-1" v 0.01 (эй-эйч-эм-би-один).
____Ниже представлена схема, которую имеем на данный момент, есть замечания, пожелания, вопросы, предложения, желание пообщатьс на эту тему, пишите:
.
____Итак, что мы имеем, после просчёта задержек распространения сигнала, вышло, что есть смысл применить условный сумматор в 5, 6 и 7 тетрадах. Хотя условным его сложно назвать, так как внутри каждой микросхемы находится параллельный сумматор с параллельным переносом, внешне именно в этих тетрадах реализован условный сумматор, ну а между частью тетрад реализован последовательный перенос. Поэтому правльно будет назвать, что у нас получился комбинированный сумматор.
____Изначально планировалось применение мультиплексоров КП16, а именно их импортных аналогов в серии 74AC (CD74AC157M), у которого время выбора входа 1,5 нс, а время прохождения данных с входа на выход 2,1 нс. Но так как по быстродействию больший эффект даёт уменьшение времени выбора входа, то решено было посмотреть на КП11, а именно CD74AC257M, у неё время выбора входа 1,1 нс, а время прохождения данных с входа на выход 2,3 нс. Конечно же, если бы этих зедержек не было бы, то всё было бы просто супер классно, но к сожалению мы живём в реальном мире, а не в идеальном, где существуют идеальные параметры...
____В результате, минимальное время получения результата в последней, восьмой тетраде, которое мы можем получить на модернизированном сумматоре, естественно при условии, идеального монтажа, соблюдения всех рекомендаций из datasheet для получения минимального времени распространения сигнала и при очень качественных образцах самих микросхем, это 14,1 нс. То есть по сравнению с предыдущей версией нашего сумматора, которая имела этот параметр равным 18,8 нс, мы получили выигрыш в 4,7 нс. Но и количество микросхем возросло с 10 до 16, что я считаю приемлемым. В результате имеем предварительно-окончательную схему сумматора I0Adder3. Так же было решено дать название, прибору, устройству, да не суть важно. "Асинхронный Hard майнер биткоина" или по английски, но в виде аббревиатуры "AHMB-1" v 0.01 (эй-эйч-эм-би-один).
____Ниже представлена схема, которую имеем на данный момент, есть замечания, пожелания, вопросы, предложения, желание пообщатьс на эту тему, пишите:

.
Viktor2312- RIP
- Сообщения : 15492
Дата регистрации : 2012-08-10
Возраст : 45
Откуда : Пятигорск
 .
.
13
Продолжим, попробуем немного поразбираться...
PREPROCESSING (ПРЕДВАРИТЕЛЬНАЯ ОБРАБОТКА).
Preprocessing consists of three steps: padding the message, M (Sec. 1), parsing the message into message blocks (Sec. 2), and setting the initial hash value, H(0) (Sec. 3).
Предварительная обработка состоит из трёх этапов: заполнение сообщения M (раздел 1), разбор сообщения на блоки сообщений (раздел 2) и установка начального значения хеш-функции H(0) (раздел 3).
1. Padding the Message (Заполнение сообщения).
The purpose of this padding is to ensure that the padded message is a multiple of 512 or 1024 bits, depending on the algorithm.
(Цель этого заполнения - гарантировать, что заполненное сообщение кратно 512 или 1024 битам, в зависимости от алгоритма.)
Padding can be inserted before hash computation begins on a message, or at any other time during the hash computation prior to processing the block(s) that will contain the padding.
(Заполнение может быть вставлено до начала вычисления хэша в сообщении или в любое другое время во время вычисления хэша до обработки блока (ов), который будет содержать заполнение.)
1.1 SHA-1, SHA-224 and SHA-256.
Suppose that the length of the message, M, is L bits. (Предположим, что длина сообщения M составляет L бит.)
Append the bit “1” to the end of the message, followed by k zero bits, where k is the smallest, non-negative solution to the equation L + 1 + k≡448mod512.
(Добавьте бит «1» в конец сообщения, за которым следуют k нулевых битов, где k - наименьшее неотрицательное решение уравнения L + 1 + k≡448mod512).
Then append the 64-bit block that is equal to the number L expressed using a binary representation.
(Затем добавьте 64-битный блок, который равен числу L, выраженному в двоичном представлении. )
For example, the (8-bit ASCII) message “abc” has length 8 × 3 = 24, so the message is padded with a one bit, then 448 - (24 + 1) = 423 zero bits, and then the message length, to become the 512-bit padded message
(Например, сообщение «abc» (8-битный ASCII) имеет длину 8 × 3 = 24, затем сообщение дополняется одним битом, и далее 448 - (24 + 1) = 423 нулевых бита, а затем длина сообщения , чтобы стать 512-битным дополненным сообщением)
The length of the padded message should now be a multiple of 512 bits.
(Длина дополненного сообщения теперь должна быть кратной 512 битам.)
2. Parsing the Message (Разбор сообщения).
The message and its padding must be parsed into N m-bit blocks.
(Сообщение и его заполнение должны быть разбиты на N m-битовых блоков.)
For SHA-1, SHA-224 and SHA-256, the message and its padding are parsed into N 512-bit blocks, M(1), M(2),…, M(N).
(Для SHA-1, SHA-224 и SHA-256 сообщение и его заполнение разбираются на N 512-битных блоков, M(1), M(2),…, M(N).)
Since the 512 bits of the input block may be expressed as sixteen 32-bit words, the first 32 bits of message block i are denoted M0(i), the next 32 bits are M1(i), and so on up to M15(i).
(Поскольку 512 битов входного блока могут быть выражены как шестнадцать 32-битных слов, первые 32 бита блока сообщения i обозначаются M0(i), следующие 32 бита - M1(i) и так далее до M15(i))
3. Setting the Initial Hash Value (H(0)) (Установка начального значения хеширования (H(0)).
Before hash computation begins for each of the secure hash algorithms, the initial hash value, H(0), must be set. The size and number of words in H(0) depends on the message digest size.
(Перед началом вычисления хеш-функции для каждого из алгоритмов безопасного хеширования необходимо установить начальное значение хеш-функции H(0). Размер и количество слов в H(0) зависит от размера дайджеста сообщения)
For SHA-256, the initial hash value, H(0), shall consist of the following eight 32-bit words, in hex:
(Для SHA-256 начальное хеш-значение H(0) должно состоять из следующих восьми 32-битных слов в шестнадцатеричном формате)
H0(0) = 6a09e667
H1(0) = bb67ae85
H2(0) = 3c6ef372
H3(0) = a54ff53a
H4(0) = 510e527f
H5(0) = 9b05688c
H6(0) = 1f83d9ab
H7(0) = 5be0cd19
Сравниваем с первым постом:
h0 := 0x6A09E667
h1 := 0xBB67AE85
h2 := 0x3C6EF372
h3 := 0xA54FF53A
h4 := 0x510E527F
h5 := 0x9B05688C
h6 := 0x1F83D9AB
h7 := 0x5BE0CD19
These words were obtained by taking the first thirty-two bits of the fractional parts of the square roots of the first eight prime numbers.
(Эти слова были получены путем взятия первых тридцати двух битов дробных частей квадратных корней из первых восьми простых чисел.)
Думаем, перевариваем, осмысливаем...
PREPROCESSING (ПРЕДВАРИТЕЛЬНАЯ ОБРАБОТКА).
Preprocessing consists of three steps: padding the message, M (Sec. 1), parsing the message into message blocks (Sec. 2), and setting the initial hash value, H(0) (Sec. 3).
Предварительная обработка состоит из трёх этапов: заполнение сообщения M (раздел 1), разбор сообщения на блоки сообщений (раздел 2) и установка начального значения хеш-функции H(0) (раздел 3).
1. Padding the Message (Заполнение сообщения).
The purpose of this padding is to ensure that the padded message is a multiple of 512 or 1024 bits, depending on the algorithm.
(Цель этого заполнения - гарантировать, что заполненное сообщение кратно 512 или 1024 битам, в зависимости от алгоритма.)
Padding can be inserted before hash computation begins on a message, or at any other time during the hash computation prior to processing the block(s) that will contain the padding.
(Заполнение может быть вставлено до начала вычисления хэша в сообщении или в любое другое время во время вычисления хэша до обработки блока (ов), который будет содержать заполнение.)
1.1 SHA-1, SHA-224 and SHA-256.
Suppose that the length of the message, M, is L bits. (Предположим, что длина сообщения M составляет L бит.)
Append the bit “1” to the end of the message, followed by k zero bits, where k is the smallest, non-negative solution to the equation L + 1 + k≡448mod512.
(Добавьте бит «1» в конец сообщения, за которым следуют k нулевых битов, где k - наименьшее неотрицательное решение уравнения L + 1 + k≡448mod512).
Then append the 64-bit block that is equal to the number L expressed using a binary representation.
(Затем добавьте 64-битный блок, который равен числу L, выраженному в двоичном представлении. )
For example, the (8-bit ASCII) message “abc” has length 8 × 3 = 24, so the message is padded with a one bit, then 448 - (24 + 1) = 423 zero bits, and then the message length, to become the 512-bit padded message
(Например, сообщение «abc» (8-битный ASCII) имеет длину 8 × 3 = 24, затем сообщение дополняется одним битом, и далее 448 - (24 + 1) = 423 нулевых бита, а затем длина сообщения , чтобы стать 512-битным дополненным сообщением)
The length of the padded message should now be a multiple of 512 bits.
(Длина дополненного сообщения теперь должна быть кратной 512 битам.)
2. Parsing the Message (Разбор сообщения).
The message and its padding must be parsed into N m-bit blocks.
(Сообщение и его заполнение должны быть разбиты на N m-битовых блоков.)
For SHA-1, SHA-224 and SHA-256, the message and its padding are parsed into N 512-bit blocks, M(1), M(2),…, M(N).
(Для SHA-1, SHA-224 и SHA-256 сообщение и его заполнение разбираются на N 512-битных блоков, M(1), M(2),…, M(N).)
Since the 512 bits of the input block may be expressed as sixteen 32-bit words, the first 32 bits of message block i are denoted M0(i), the next 32 bits are M1(i), and so on up to M15(i).
(Поскольку 512 битов входного блока могут быть выражены как шестнадцать 32-битных слов, первые 32 бита блока сообщения i обозначаются M0(i), следующие 32 бита - M1(i) и так далее до M15(i))
3. Setting the Initial Hash Value (H(0)) (Установка начального значения хеширования (H(0)).
Before hash computation begins for each of the secure hash algorithms, the initial hash value, H(0), must be set. The size and number of words in H(0) depends on the message digest size.
(Перед началом вычисления хеш-функции для каждого из алгоритмов безопасного хеширования необходимо установить начальное значение хеш-функции H(0). Размер и количество слов в H(0) зависит от размера дайджеста сообщения)
For SHA-256, the initial hash value, H(0), shall consist of the following eight 32-bit words, in hex:
(Для SHA-256 начальное хеш-значение H(0) должно состоять из следующих восьми 32-битных слов в шестнадцатеричном формате)
H0(0) = 6a09e667
H1(0) = bb67ae85
H2(0) = 3c6ef372
H3(0) = a54ff53a
H4(0) = 510e527f
H5(0) = 9b05688c
H6(0) = 1f83d9ab
H7(0) = 5be0cd19
Сравниваем с первым постом:
h0 := 0x6A09E667
h1 := 0xBB67AE85
h2 := 0x3C6EF372
h3 := 0xA54FF53A
h4 := 0x510E527F
h5 := 0x9B05688C
h6 := 0x1F83D9AB
h7 := 0x5BE0CD19
These words were obtained by taking the first thirty-two bits of the fractional parts of the square roots of the first eight prime numbers.
(Эти слова были получены путем взятия первых тридцати двух битов дробных частей квадратных корней из первых восьми простых чисел.)
Думаем, перевариваем, осмысливаем...
Viktor2312- RIP
- Сообщения : 15492
Дата регистрации : 2012-08-10
Возраст : 45
Откуда : Пятигорск
 .
.
14
Разработка модуля Maj первой итерации.
Для краткости мы Maj первой итерации, сократим до MaI1 (не забываем, что у нас счёт идёт от нуля).
Как уже было сказано/написано:
(Ну вот ситуация уже улучшается, NC7SV08 это AND на два входа, это так называемая Tiny Logic ULP-A. А главное те задержки, что у 74AC максимально достижимы 2 нс. Тут являются самыми худшими параметрами, если уж совсем всё плохо. А типовое значение задержки распространения сигнала 1 нс. И питание 3,3 В. Я уже думал, что нужно однозначно переходить на 3,3 В, это как минимум позволяет кардинально уменьшить потребление. В общим серия ULP-A мне гарантировано даёт ещё х2 в быстродействии. И оформлена она, по одному логическому элементу в корпусе, что хорошо. Так как у нас как раз таки работа будет с каждым битом в отдельности, и если выходит повторитель, то ничего не ставим, если инвертор, то и ставим один логический элемент NOT и получаем наши заветные 1 нс, а в идеале и 0,7 нс, если не напортачить с ёмкостью монтажа и нагрузкой.
Поэтому я сегодня решил заняться разработкой блока Maj для второй итерации. Рисунок для наглядности и понимания сути:
Как видим на блок Maj поступает три слова A, B, C это 32-разрядные слова, и напомню, что мы блок будем делать для второй итерации, а соответственно слова B и C нам известны, они константы приходящие от первой итерации, а по сути просто проходящие через неё без каких либо изменений, что можно посмотреть на рисунке выше. A идёт на B, B идёт на C. И таким образом мы имеем, что A у нас неизвестная переменная, B = A(0 итерации) = 0x6A09E667 и С = B(0итерации) = 0xBB67AE85
В самом же блоке Maj происходит следующее:
Функция большинства (Maj блок) побитово работает со словами A, B и C. Для каждой битовой позиции она возвращает 0, если большинство входных битов в этой позиции — нули, иначе вернёт 1.
Ma := (a and b) xor (a and c) xor (b and c)
Но мы же уже воспользовались оптимизацией, а именно:
Закон дистрибутивности. Дистрибутивность конъюнкции и суммы по модулю два.
(a and b) xor (a and c) = a and (b xor c)
И соответственно имеем:
(a and (b xor c)) xor (b and c)
Что нам это дало, в первом случае у нас 5 логических операций, три and и две xor
Теперь же четыре, меньше на один and, а это в случае трёх неизвестных переменных экономит 32 микросхемы NC7SV08. Тут мы в первом случае сделали бы три and параллельно, потом первый xor и затем второй. Сейчас то же самое по количеству квантов времени, тоже три делаем xor и and параллельно, и затем and и xor.
Но, что же в нашем случае, благодаря ручной обработке?
b xor c и b and с
А они нам известны, а о чём это говорит, а об много, что схема будет максимально компактной, малопотребляющей и скоростной...
Ну а дальше, уже не интересно, дальше разработка...
NC7SV08 datasheet)
Дальнейшая разработка будет продолжена с этого места, ниже:
Итак продолжим. У нас имеется:
Maj = (a and (b xor c)) xor (b and c),
а так же:
b = 0x6A09E667
c = 0xBB67AE85
Вычисляем (b and c) и получаем 0x2A01A605 (0010 1010 0000 0001 1010 0110 0000 0101).
Вычисляем (b xor c) и получаем 0xD16E48E2 (1101 0001 0110 1110 0100 1000 1110 0010)
Теперь имеем:
MaI1 = (a and 0xD16E48E2) xor 0x2A01A605
Итак, подведём кратенький итог, из 5-ти логических операций (а это потребовало бы 160 логических элементов или 160 микросхем серии NC7SVxx), сначала мы преобразовали до 4-х логических операций и затем, благодаря константам пришли к 2-м логическим операциям. Кажется в нашем огромном шкафу, как тут выразился один человек, стало попросторнее, даже если оставить как есть на этом этапе, то это 64 микросхемы. Для того, чтобы никто не пугался цифрам, и для тех кто не открыл ссылку на datasheet замечу, что одна микросхема имеет размеры 2 х 2 х 1 мм.
Но, мы будем и дальше избавляться от лишних микросхем!
Далее рассматриваем первую логическую операцию и создаём схему:
a and 0xD16E48E2 (1101 0001 0110 1110 0100 1000 1110 0010)
0 - a and 0 = 0 (так как на одном из входов присутствует всехда лог. 0, то на выходе будет всегда лог. 0)
Это значит, во-первых, что нам не нужен логический элемент (в шкафу становится ещё просторнее) мы просто для следующей операции, а у нас это (наш результат xor 0x2A01A605) в данном бите получаем константу равную лог. 0 и как следствие в дальнейшем выкинет ещё один логический элемент xor в виду того, что если на одном входе всегда лог. 0 то xor превращается в повторитель.
0 - a and 0 = 0
1 - a and 1 = повторитель (нет лог. элемента сигнал на прямую проходит до xor)
2 - a and 0 = 0
3 - a and 0 = 0
4 - a and 0 = 0
5 - a and 1 = повторитель
6 - a and 1 = повторитель
7 - a and 1 = повторитель
8 - a and 0 = 0
9 - a and 0 = 0
10 - a and 0 = 0
11 - a and 1 = повторитель
12 - a and 0 = 0
13 - a and 0 = 0
14 - a and 1 = повторитель
15 - a and 0 = 0
16 - a and 0 = 0
17 - a and 1 = повторитель
18 - a and 1 = повторитель
19 - a and 1 = повторитель
20 - a and 0 = 0
21 - a and 1 = повторитель
22 - a and 1 = повторитель
23 - a and 0 = 0
24 - a and 1 = повторитель
25 - a and 0 = 0
26 - a and 0 = 0
27 - a and 0 = 0
28 - a and 1 = повторитель
29 - a and 0 = 0
30 - a and 1 = повторитель
31 - a and 1 = повторитель
Ну вот, выкинулись все 32 логических элемента, 32 конденсатора, часть бит пройдут напрямую, а нулевые биты вообще, это "земля".
И далее:
0x2A01A605 (0010 1010 0000 0001 1010 0110 0000 0101)
На выходе блока MaI1 имеем:
0 - лог.1
1 - a (первый бит числа a)
2 - лог.1
3 - лог.0
4 - лог.0
5 - a (пятый бит числа a)
6 - a (шестой бит числа a)
7 - a (седьмой бит числа a)
8 - лог.0
9 - лог.1
10 - лог.1
11 - a (одинадцатый бит числа a)
12 - лог.0
13 - лог.1
14 - a (четырнадцатый бит числа a)
15 - лог.1
16 - лог.1
17 - a (семнадцатый бит числа a)
18 - a (восемнадцатый бит числа a)
19 - a (девятнадцатый бит числа a)
20 - лог.0
21 - a (двадцать первый бит числа a)
22 - a (двадцать второй бит числа a)
23 - лог.0
24 - a (двадцать четвёртый бит числа a)
25 - лог.1
26 - лог.0
27 - лог.1
28 - a (двадцать восьмой бит числа a)
29 - лог.1
30 - a (тридцатый бит числа a)
31 - a (тридцать первый бит числа a)
Всё. Подведём окончательный итог. Количество необходимых микросхем 0 шт. блокировочных конденсаторов 0 шт. Задержка сигнала в блоке MaI1 равна 0 нс. Думаю результат отличный!
- Спойлер:
.
Viktor2312- RIP
- Сообщения : 15492
Дата регистрации : 2012-08-10
Возраст : 45
Откуда : Пятигорск
 .
.
15
Оставлю тут, как памятку, так как ещё не определился до конца с логикой, и нашлось много очень скоростной логики:
AHCT - Улучшенная высокоскоростная CMOS, совместимая по выходам с биполярными сериями;
ALVC - с низким напряжением питания (1,65 - 3,3В), время срабатывания 2 нс;
AUC - с низким напряжением питания (0.8 - 2,7В), время срабатывания < 1,9 нс при Vпит=1,8В;
FC - быстрая CMOS, скорость аналогична F;
FCT - быстрая CMOS, совместимая по выходам с биполярными сериями;
LCX - CMOS с питанием 3В и 5В-совместимыми входами;
LVC - с пониженным напряжением (1,65 - 3.3В) и 5В-совместимыми входами, время срабатывания < 5,5 нс при Vпит=3,3V, < 9 нс при Vпит=2,5В;
LVQ - с пониженным напряжением (3,3В);
LVX - с питанием 3,3В и 5В-совместимыми входами;
VHC - Сверхвысокоскоростная CMOS - быстродействие сравнимо с S;
VHCT - Сверхвысокоскоростная CMOS, совместимая по выходам с биполярными сериями;
G - Супер-сверхвысокоскоростная для частот выше 1 ГГц, питание 1,65В - 3,3В, 5В-совместимые входы;
BCT - BiCMOS, TTL-совместимые входы, используется для буферов;
ABT - УлучшеннаяBiCMOS, TTL-совместимые входы, быстрее ACT и BCT;
Для более гибкого применения существует также серия от NXP(74LVC1G***) и TI (SN74LVC1G***), где всего 1 логический элемент в 5 6-ти выводном корпусе, для конструкций с малым количеством разных элементов и минимальным размером платы. Например: 74LVC1G00GW SOT353-1 Single 2-Input Positive-AND Gate (NXP)
И вот посмотрев сейчас на Итерацию 0, где мне требуется пусть и упрощённых, но 3 сумматора, я решил подумать и до меня дошло, что там закралось ещё одно сложение с двумя известными константами, это значение после Adder2 и значение входного D.

В результате сложив их, нам для получения выходного E, потребуется к результату просто прибавить Wi [0]. Так же и со вторым сумматором. В итоге в итерации 0 потребуется всего два упрощённых сумматора, упрощённых, потому, что один из операндов нам известен.
В итоге придётся все переразрабатывать, учитывая это, зато убирается ещё куча "железа" и экономия в потреблении, и с учётом найденной новой скоростной и доступной логики NC7SV. Это всё очень хорошо скажется на быстродействии!
И в итоге имеем материал для работы над оставшимися двумя упрощёнными сумматорами, которые и будут уже реализованы в железе, посмотрим, может благодаря логике NC7SV получится избавиться, хотя бы частично от относительно медленных 74AC283...
.
AHCT - Улучшенная высокоскоростная CMOS, совместимая по выходам с биполярными сериями;
ALVC - с низким напряжением питания (1,65 - 3,3В), время срабатывания 2 нс;
AUC - с низким напряжением питания (0.8 - 2,7В), время срабатывания < 1,9 нс при Vпит=1,8В;
FC - быстрая CMOS, скорость аналогична F;
FCT - быстрая CMOS, совместимая по выходам с биполярными сериями;
LCX - CMOS с питанием 3В и 5В-совместимыми входами;
LVC - с пониженным напряжением (1,65 - 3.3В) и 5В-совместимыми входами, время срабатывания < 5,5 нс при Vпит=3,3V, < 9 нс при Vпит=2,5В;
LVQ - с пониженным напряжением (3,3В);
LVX - с питанием 3,3В и 5В-совместимыми входами;
VHC - Сверхвысокоскоростная CMOS - быстродействие сравнимо с S;
VHCT - Сверхвысокоскоростная CMOS, совместимая по выходам с биполярными сериями;
G - Супер-сверхвысокоскоростная для частот выше 1 ГГц, питание 1,65В - 3,3В, 5В-совместимые входы;
BCT - BiCMOS, TTL-совместимые входы, используется для буферов;
ABT - УлучшеннаяBiCMOS, TTL-совместимые входы, быстрее ACT и BCT;
Для более гибкого применения существует также серия от NXP(74LVC1G***) и TI (SN74LVC1G***), где всего 1 логический элемент в 5 6-ти выводном корпусе, для конструкций с малым количеством разных элементов и минимальным размером платы. Например: 74LVC1G00GW SOT353-1 Single 2-Input Positive-AND Gate (NXP)
И вот посмотрев сейчас на Итерацию 0, где мне требуется пусть и упрощённых, но 3 сумматора, я решил подумать и до меня дошло, что там закралось ещё одно сложение с двумя известными константами, это значение после Adder2 и значение входного D.

В результате сложив их, нам для получения выходного E, потребуется к результату просто прибавить Wi [0]. Так же и со вторым сумматором. В итоге в итерации 0 потребуется всего два упрощённых сумматора, упрощённых, потому, что один из операндов нам известен.
В итоге придётся все переразрабатывать, учитывая это, зато убирается ещё куча "железа" и экономия в потреблении, и с учётом найденной новой скоростной и доступной логики NC7SV. Это всё очень хорошо скажется на быстродействии!
И в итоге имеем материал для работы над оставшимися двумя упрощёнными сумматорами, которые и будут уже реализованы в железе, посмотрим, может благодаря логике NC7SV получится избавиться, хотя бы частично от относительно медленных 74AC283...
.
Viktor2312- RIP
- Сообщения : 15492
Дата регистрации : 2012-08-10
Возраст : 45
Откуда : Пятигорск
 .
.
16
Ну вот и пришло время разработать "Параллельный сумматор с параллельным переносом" с использованием NC7SV серии микросхем с типовой задержкой 1,0 нс и питанием 3,3 В. На минимальную 0,7 нс думаю рассчитывать не стоит.
Итак, у нас есть A и B, главное, что у нас сложение по модулю 32 и нам не нужен бит переноса в младший разряд, он всегда равен лог. 0, а так же нам не нужен бит переноса P31 в 32 разряд, так как он отбрасывается. Это всё убирает огромное количество логических элементов, а так как в серии NC7SV каждый элемент оформлен в виде отдельной микросхемы, то и логично, что у нас уменьшается количество микросхем и блокировочных конденсаторов, которые кстати по габаритам почти как сама микросхема. Ну и бонусом у нас, нам известна B, что ещё отбросит большое количество микросхем.
Для построения мы будем использовать однобитный сумматор, изначально на двух элементах XOR "исключающее ИЛИ", но так как B нам известно, то в зависимости от того чему равен конкретный бит, это превращает один из элементов XOR либо в повторитель, и соответственно исключает его из схемы, либо в инвертор, в качестве инвертора мы будем применять NC7SV00 (ЛА3 - 2И-НЕ) из-за её более лучших параметров по быстродействию.
И естественно без бита переноса, так как для каждого бита переноса будет строиться отдельная схема.
Суть посмотреть какая получится задержка, так как элементы имеют мало входов, два, их придётся наращивать, и тут каждая ступень будет добавлять задержку в 1 нс., к сожалению, но просчитав предварительно, что при построении элемента 20И-НЕ выходит задержка 5 нс, что вполне приемлемо, с XOR в сумматоре 6 нс, но посмотрим как оно будет, притом в отличии от 74AC где мы руководствовались минимальной задержкой, максимально достижимой 1...2 нс, по сути сферическим конём в вакууме, то тут мы пользуемся типовым значением 1,0 нс.
Однобитный сумматор, построенный на двух логических элементах XOR без бита переноса в старший разряд:
Далее представим наглядно наше числи B которое у нас равно 0xFC08884D в двоичной системе:
И начнём построение и расчёт схемы с нулевого бита. А так как P у нас равен лог. 0 всегда, то элемент D1 превращается в повторитель и просто убирается из схемы, а элемент D2 из-за того, что b0 равен лог. 1 превращается в инвертор. И по сути у нас остаётся только один инвертор.
Сразу стоит уточнить, мы не будем превышать нагрузочную способность более чем N=10, поэтому возможно из-за этого потребуется немного дополнительных микросхем, для буферизации.
В итоге имеем:
Теперь нам необходимо составить схему для бита переноса P0, но предварительно нам нужно вычислить все коэффициенты hi. по формуле:
Но проще её преобразовать до: hi = ai or bi
И так как у нас B известно, то h будет равна либо лог. 1, когда bi равна лог. 1, либо самому ai, итак находим все hi
h0 = 1
h1 = a1
h2 = 1
h3 = 1
h4 = a4
h5 = a5
h6 = 1
h7 = a7
h8 = a8
h9 = a9
h10 = a10
h11 = 1
h12 = a12
h13 = a13
h14 = a14
h15 = 1
h16 = a16
h17 = a17
h18 = a18
h19 = 1
h20 = a20
h21 = a21
h22 = a22
h23 = a23
h24 = a24
h25 = a25
h26 = 1
h27 = 1
h28 = 1
h29 = 1
h30 = 1
h31 = 1
И теперь перед началом расчётов и разработке схемы далее, основная формула для вычисления и построения схемы переноса для конкретного бита:
Как видно из формулы, в последней её части присутствует наш бит переноса в младший разряд, а он у нас всегда равен лог. 0, что в данной части формулы нам всегда даст лог. 1 на выходе логического элемента построенного по этой формуле. Поэтому эта часть у нас и отпадает, сокращается.
И для P0 мы имеем:
И что мы имеем в итоге? Правая часть формулы из-за P превращается в лог. 1 и делает второй логический элемент инвертором. Чтобы было понятнее, поясню, первая часть формулы, это логический элемент 2И-НЕ, вторая тоже, и верхняя чёрточка инверсии, это третий логический элемент:
В результате нижний по схеме логический элемент из-за P на выходе будет всегда иметь лог. 1 вне зависимости от того чему будет равно h0, верхний логический элемент из-за b0 = лог. 1 превращается в инвертор, и последний логический элемент становится инвертором, из-за лог. 1 приходящей с нижнего логического элемента, в итоге получается, что сигнал a0 проходит через два инвертора. Смысла в этом нет, так как:
a0 -> /a0 -> a0 то мы можем напрямую подать сигнал a0 на выход, то есть имеем: P0 = a0.
Далее сумматор следующего бита. Нижний по схеме элемент XOR (a1 xor b1) из-за того, что b1 = 0 становится повторителем и исключается из схемы за ненужностью, второй остаётся, на который и подаются P0 и a1 и схема становится такой:
Переходим к расчёту бита переноса P1
Первая часть формулы из-за b1 = 0 создаёт лог. 1 на входе третьего логического элемента и делает его инвертором, вторая часть формулы имеет два входа с a0 и a1 и так как у нас образуется две подряд инверсии, то вся формула приводит нас к логическому элементу И (and), в качестве которого у нас будет выступать микросхема NC7SV08. И дополняем схему:
Далее переходим к сумматору второго разряда (нулевой и первый готовы). b2 = 1, что делает нижний по схеме элемент инвертором, второй остаётся без изменений. Наносим на схему:
И переходим к расчёту бита переноса P2.
Теперь наносим на схему, но сигнал a2 у нас уже имеется инвертированный, поэтому это нам сэкономит логические элементы, главное следить, N=10 не более...
И переходим к сумматору третьего разряда (0, 1, 2 - готовы). Здесь всё как и в предыдущем случае, b3 = 1 соответственно нижний элемент XOR становится инвертором, верхний остаётся. И наносим на схему:
Переходим к биту переноса P3, формула, схема, упрощаем схему, если посмотреть на /a3 который мы должны получить, и хоть он у нас уже имеется, в данной части схемы он не пригодится, что хорошо, а не пригодтся из-за того, что в первом случае у нас элемент 2И-НЕ становится инвертором, а во втором случае, благодаря наращиванию, то есть получению логического элемента 4И-НЕ, второй элемент (2И-НЕ) составного элемента 4И-НЕ имеет один вход свободный, куда нам нужно подать лог. 1, что превращает его по сути в инвертор и как следствие сигнал /a3 проходит через два инвертора, а значит мы его можем сразу подавать на объединяющий логический элемент ИЛИ (or). Вот что имеем:
И наносим на схему:
В качестве логического элемента ИЛИ (or) будет использоваться микросхема NC7SV32 с типовым значением времени задержки распространения сигнала 1,0 нс.
Движемся дальше, делаем сумматор для S4. Так как b4 = 0 то нижний элемент xor становится повторителем и исключается, на второй элемент xor приходят соответственно P3 и a4, чертим:
И переходим к расчёту P4.
Ну вот, прогулялся, сигаретками до понедельника втарился, бутылочку пивка выпил, свежим воздухом подышал, ляпота, курочка пусть размораживается, а пока, продолжим. P4 всё по формуле и т. д.
И наносим на схему:
Переходим к сумматору пятого разряда a5 и b5, у нас b5 = 0. Соответственно нижний элемент XOR становится повторителем и исключается, а на верхний приходят P4 и a5. Наносим на схему:
И переходим к расчёту P5.
И чертим:
Курочка жарится, я весь в предвкушении киношки с вкусняшками, ааа ароматы, но и пусть жарится, считаем сумматор шестого разряда, на нижний элемент XOR приходят a6 и b6, у нас b6 = 1, соответственно XOR становится инвертором, и ничего страшного, нам всё равно потребуется инверный шестой бит, на верхний элемент XOR приходит бит переноса P5 и соответственно наш /a6, задержка по S6 составит 5 нс. Чертим:
И переходим к расчёту P6.
Ииии, и на сегодня хватит, курочка, фильма, да и мой мозг уже косо на меня смотрит, с намёком может хватит уже, завтра продолжу, но чем больше разрядов, тем больше, короче, дальше в лес - больше дров!
.
Итак, у нас есть A и B, главное, что у нас сложение по модулю 32 и нам не нужен бит переноса в младший разряд, он всегда равен лог. 0, а так же нам не нужен бит переноса P31 в 32 разряд, так как он отбрасывается. Это всё убирает огромное количество логических элементов, а так как в серии NC7SV каждый элемент оформлен в виде отдельной микросхемы, то и логично, что у нас уменьшается количество микросхем и блокировочных конденсаторов, которые кстати по габаритам почти как сама микросхема. Ну и бонусом у нас, нам известна B, что ещё отбросит большое количество микросхем.
Для построения мы будем использовать однобитный сумматор, изначально на двух элементах XOR "исключающее ИЛИ", но так как B нам известно, то в зависимости от того чему равен конкретный бит, это превращает один из элементов XOR либо в повторитель, и соответственно исключает его из схемы, либо в инвертор, в качестве инвертора мы будем применять NC7SV00 (ЛА3 - 2И-НЕ) из-за её более лучших параметров по быстродействию.
И естественно без бита переноса, так как для каждого бита переноса будет строиться отдельная схема.
Суть посмотреть какая получится задержка, так как элементы имеют мало входов, два, их придётся наращивать, и тут каждая ступень будет добавлять задержку в 1 нс., к сожалению, но просчитав предварительно, что при построении элемента 20И-НЕ выходит задержка 5 нс, что вполне приемлемо, с XOR в сумматоре 6 нс, но посмотрим как оно будет, притом в отличии от 74AC где мы руководствовались минимальной задержкой, максимально достижимой 1...2 нс, по сути сферическим конём в вакууме, то тут мы пользуемся типовым значением 1,0 нс.
Однобитный сумматор, построенный на двух логических элементах XOR без бита переноса в старший разряд:
Далее представим наглядно наше числи B которое у нас равно 0xFC08884D в двоичной системе:
И начнём построение и расчёт схемы с нулевого бита. А так как P у нас равен лог. 0 всегда, то элемент D1 превращается в повторитель и просто убирается из схемы, а элемент D2 из-за того, что b0 равен лог. 1 превращается в инвертор. И по сути у нас остаётся только один инвертор.
Сразу стоит уточнить, мы не будем превышать нагрузочную способность более чем N=10, поэтому возможно из-за этого потребуется немного дополнительных микросхем, для буферизации.
В итоге имеем:
Теперь нам необходимо составить схему для бита переноса P0, но предварительно нам нужно вычислить все коэффициенты hi. по формуле:
Но проще её преобразовать до: hi = ai or bi
И так как у нас B известно, то h будет равна либо лог. 1, когда bi равна лог. 1, либо самому ai, итак находим все hi
h0 = 1
h1 = a1
h2 = 1
h3 = 1
h4 = a4
h5 = a5
h6 = 1
h7 = a7
h8 = a8
h9 = a9
h10 = a10
h11 = 1
h12 = a12
h13 = a13
h14 = a14
h15 = 1
h16 = a16
h17 = a17
h18 = a18
h19 = 1
h20 = a20
h21 = a21
h22 = a22
h23 = a23
h24 = a24
h25 = a25
h26 = 1
h27 = 1
h28 = 1
h29 = 1
h30 = 1
h31 = 1
И теперь перед началом расчётов и разработке схемы далее, основная формула для вычисления и построения схемы переноса для конкретного бита:
Как видно из формулы, в последней её части присутствует наш бит переноса в младший разряд, а он у нас всегда равен лог. 0, что в данной части формулы нам всегда даст лог. 1 на выходе логического элемента построенного по этой формуле. Поэтому эта часть у нас и отпадает, сокращается.
И для P0 мы имеем:
И что мы имеем в итоге? Правая часть формулы из-за P превращается в лог. 1 и делает второй логический элемент инвертором. Чтобы было понятнее, поясню, первая часть формулы, это логический элемент 2И-НЕ, вторая тоже, и верхняя чёрточка инверсии, это третий логический элемент:
В результате нижний по схеме логический элемент из-за P на выходе будет всегда иметь лог. 1 вне зависимости от того чему будет равно h0, верхний логический элемент из-за b0 = лог. 1 превращается в инвертор, и последний логический элемент становится инвертором, из-за лог. 1 приходящей с нижнего логического элемента, в итоге получается, что сигнал a0 проходит через два инвертора. Смысла в этом нет, так как:
a0 -> /a0 -> a0 то мы можем напрямую подать сигнал a0 на выход, то есть имеем: P0 = a0.
Далее сумматор следующего бита. Нижний по схеме элемент XOR (a1 xor b1) из-за того, что b1 = 0 становится повторителем и исключается из схемы за ненужностью, второй остаётся, на который и подаются P0 и a1 и схема становится такой:
Переходим к расчёту бита переноса P1
Первая часть формулы из-за b1 = 0 создаёт лог. 1 на входе третьего логического элемента и делает его инвертором, вторая часть формулы имеет два входа с a0 и a1 и так как у нас образуется две подряд инверсии, то вся формула приводит нас к логическому элементу И (and), в качестве которого у нас будет выступать микросхема NC7SV08. И дополняем схему:
Далее переходим к сумматору второго разряда (нулевой и первый готовы). b2 = 1, что делает нижний по схеме элемент инвертором, второй остаётся без изменений. Наносим на схему:
И переходим к расчёту бита переноса P2.
Теперь наносим на схему, но сигнал a2 у нас уже имеется инвертированный, поэтому это нам сэкономит логические элементы, главное следить, N=10 не более...
И переходим к сумматору третьего разряда (0, 1, 2 - готовы). Здесь всё как и в предыдущем случае, b3 = 1 соответственно нижний элемент XOR становится инвертором, верхний остаётся. И наносим на схему:
Переходим к биту переноса P3, формула, схема, упрощаем схему, если посмотреть на /a3 который мы должны получить, и хоть он у нас уже имеется, в данной части схемы он не пригодится, что хорошо, а не пригодтся из-за того, что в первом случае у нас элемент 2И-НЕ становится инвертором, а во втором случае, благодаря наращиванию, то есть получению логического элемента 4И-НЕ, второй элемент (2И-НЕ) составного элемента 4И-НЕ имеет один вход свободный, куда нам нужно подать лог. 1, что превращает его по сути в инвертор и как следствие сигнал /a3 проходит через два инвертора, а значит мы его можем сразу подавать на объединяющий логический элемент ИЛИ (or). Вот что имеем:
И наносим на схему:
В качестве логического элемента ИЛИ (or) будет использоваться микросхема NC7SV32 с типовым значением времени задержки распространения сигнала 1,0 нс.
Движемся дальше, делаем сумматор для S4. Так как b4 = 0 то нижний элемент xor становится повторителем и исключается, на второй элемент xor приходят соответственно P3 и a4, чертим:
И переходим к расчёту P4.
Ну вот, прогулялся, сигаретками до понедельника втарился, бутылочку пивка выпил, свежим воздухом подышал, ляпота, курочка пусть размораживается, а пока, продолжим. P4 всё по формуле и т. д.
И наносим на схему:
Переходим к сумматору пятого разряда a5 и b5, у нас b5 = 0. Соответственно нижний элемент XOR становится повторителем и исключается, а на верхний приходят P4 и a5. Наносим на схему:
И переходим к расчёту P5.
И чертим:
Курочка жарится, я весь в предвкушении киношки с вкусняшками, ааа ароматы, но и пусть жарится, считаем сумматор шестого разряда, на нижний элемент XOR приходят a6 и b6, у нас b6 = 1, соответственно XOR становится инвертором, и ничего страшного, нам всё равно потребуется инверный шестой бит, на верхний элемент XOR приходит бит переноса P5 и соответственно наш /a6, задержка по S6 составит 5 нс. Чертим:
И переходим к расчёту P6.
Ииии, и на сегодня хватит, курочка, фильма, да и мой мозг уже косо на меня смотрит, с намёком может хватит уже, завтра продолжу, но чем больше разрядов, тем больше, короче, дальше в лес - больше дров!
.
Viktor2312- RIP
- Сообщения : 15492
Дата регистрации : 2012-08-10
Возраст : 45
Откуда : Пятигорск
 .
.
17
Продолжу.
Наносим на схему P6.
Теперь разрабатываем сумматор для седьмого бита S7. Имеем на входе нижнего логического элемента a7 и b7, у нас b7 = 0, соответственно нижний элемент становится повторителем и исключается, остаётся верхний логический элемент XOR, на который приходят сигналы P6 и a7. Добавляем в схему:
И движемся дальше, рассчитываем P7.
Наносим на схему:
И можно подвести кратенький, промежуточный итог, так как готово восемь бит результата S0 - S7 и бит переноса P7, и результат и бит переноса имеют задержку 5 нс, что уже лучше, по сравнению с тем, что мы имели при применении 74AC283, на 1 нс по результату и на 0,4 нс по биту переноса. Но это у нас типовое значение, минимально достижимое может быть и ещё меньше, а в случае с 74AC283 то было максимально достижимое, а типовое примерно в два раза больше. И имеем мы 48 микросхем, но из-за их габаритов, это всё укладывается на платке с размерами 7 см в длину, если расположить микросхемы в 2 ряда, но о расположении на плате пока рановато думать, хотя располагать думаю нужно будет по 8 микросхем в одном ряду...
Нужно двигаться дальше.
Восьмой бит суммы S8 будет реализован на одном элементе XOR, так как b8 = 0. И будет иметь задержку 6 нс. На входы приходят соответственно P7 (5 нс) и a8. И рассчитываем P8, будет 5 нс.
...
Наносим на схему P6.
Теперь разрабатываем сумматор для седьмого бита S7. Имеем на входе нижнего логического элемента a7 и b7, у нас b7 = 0, соответственно нижний элемент становится повторителем и исключается, остаётся верхний логический элемент XOR, на который приходят сигналы P6 и a7. Добавляем в схему:
И движемся дальше, рассчитываем P7.
Наносим на схему:
И можно подвести кратенький, промежуточный итог, так как готово восемь бит результата S0 - S7 и бит переноса P7, и результат и бит переноса имеют задержку 5 нс, что уже лучше, по сравнению с тем, что мы имели при применении 74AC283, на 1 нс по результату и на 0,4 нс по биту переноса. Но это у нас типовое значение, минимально достижимое может быть и ещё меньше, а в случае с 74AC283 то было максимально достижимое, а типовое примерно в два раза больше. И имеем мы 48 микросхем, но из-за их габаритов, это всё укладывается на платке с размерами 7 см в длину, если расположить микросхемы в 2 ряда, но о расположении на плате пока рановато думать, хотя располагать думаю нужно будет по 8 микросхем в одном ряду...
Нужно двигаться дальше.
Восьмой бит суммы S8 будет реализован на одном элементе XOR, так как b8 = 0. И будет иметь задержку 6 нс. На входы приходят соответственно P7 (5 нс) и a8. И рассчитываем P8, будет 5 нс.
...
Viktor2312- RIP
- Сообщения : 15492
Дата регистрации : 2012-08-10
Возраст : 45
Откуда : Пятигорск
 .
.
18
В пи... эээ зду бухать, лучше биты шевелить!
Чё там. Чё там, у нас дальше, аааа... S9, ну поехали. Имеем a9 и b9, и b9 = 0, соответственно нижний элемент XOR становится повторителем и исключается из схемы, остаётся верхний, задержка 6 нс
Далее рассчитываем P9.
И наносим на схему, но выкинув два логических элемента, так как на одном мы получаем сигнал IS16 и его будем использовать, посмотрев внимательно на рисунок выше, можно увидеть дублирующие логические элементы.
И переходим к расчёту P10, что потребует немного больше места, из-за 10, ну да ладно это мелочи, для начала сам сумматор с a10 и b10, а b10 = 0 и поэтому всё стандартно, нижний XOR выкидываем на верхний подаём P9 и a10 и получаем S10 с задержкой 6 нс.
И переходим к расчёту P10.
Чё там. Чё там, у нас дальше, аааа... S9, ну поехали. Имеем a9 и b9, и b9 = 0, соответственно нижний элемент XOR становится повторителем и исключается из схемы, остаётся верхний, задержка 6 нс
Далее рассчитываем P9.
И наносим на схему, но выкинув два логических элемента, так как на одном мы получаем сигнал IS16 и его будем использовать, посмотрев внимательно на рисунок выше, можно увидеть дублирующие логические элементы.
И переходим к расчёту P10, что потребует немного больше места, из-за 10, ну да ладно это мелочи, для начала сам сумматор с a10 и b10, а b10 = 0 и поэтому всё стандартно, нижний XOR выкидываем на верхний подаём P9 и a10 и получаем S10 с задержкой 6 нс.
И переходим к расчёту P10.
Viktor2312- RIP
- Сообщения : 15492
Дата регистрации : 2012-08-10
Возраст : 45
Откуда : Пятигорск
 .
.
19
Ну вот, посмотрев сейчас пьяным взглядом на схему, увидел ошибку в схеме формирования P3, сигнал подан A3, а должен быть инверсный /A3 так как это заменяет элемент 2И-НЕ, и тут же вторую, так как для объединений двух 2И-НЕ, чтобы получить 4И-НЕ нужен ИЛИ, а я влепил 2И-НЕ, поправил, но это намёк, что после окончания разработки, детальная и тщательная проверка, не просто нужна, а обязательно и скрупулёзно.
Теперь так:
А теперь, вернул всё назад. Так как нефиг по пьяни суваться в схемы, и уж тем более расчёты! Сейчас перепроверил и всё там верно было.
.
Теперь так:
А теперь, вернул всё назад. Так как нефиг по пьяни суваться в схемы, и уж тем более расчёты! Сейчас перепроверил и всё там верно было.
.
Viktor2312- RIP
- Сообщения : 15492
Дата регистрации : 2012-08-10
Возраст : 45
Откуда : Пятигорск
 .
.
20
В общим, обдумывания, и т. д... привели к выводу, что схему нужно будет оптимизировать, а то, например, мы на D2 производим логическое умножение для получения P1, да с одной стороны, в отличии от применения 2И-НЕ и потом инвертора НЕ, как по формуле, просто И, уменьшаем задержку на 1 нс, до 1 нс вместо 2 нс. Но это не имеет смысла, так как всё равно в старших разрядах задержка будет больше и это нам ничего не даёт, а вот сигнал A0 nand A1 нам всё равно нужен дальше в схеме и мы всё равно его получаем на дополнительном логическом элементе D6, а так как он уже сейчас до P10 использован 8 раз, то возможно придётся и ещё ставить дополнительный элемент, чтобы иметь A0 nand A1 - 1 к которому будет подключаться 10 входов и A0 nand A1 - 2 к которому будут подключаться очередные 10 входов, чтобы соблюдать условие N=10. Чтобы не перегружать выходы и не занижать уровни выходного напряжения. Можно было бы и буферные элементы применить NC7SC125 или NC7SV126, но тут хочется сократить разнообразие микросхем, это удобно при заказе, хотя... Так как буферы всё равно потребуются, возможно лучше и их применить, а не дублировать сигналы при помощи самих элементов логических функций, как например с D6, ставится D6 и к её выходу подключаются 2...3 ... сколько нужно буферов для получения: A0 nand A1 - 1, A0 nand A1 - 2 ... A0 nand A1 - n, но точное количество будет известно только после полного расчёта схемы, а до этого ещё далеко, такими темпами.
В общим, пойду я дальше заниматься ремонтом и обдумывать, так как вот например, хотелось элементы с большим числом входов, и есть 3И-НЕ (3 input NAND), но он имеет типовую задержку 2,8 нс, что выходит на 0,8 нс медленее, чем если сделать просто составной элемент на 2И-НЕ и ИЛИ, и опять же, нужно рассчитывать схему до конца, так как в младших разрядах, возможно это будет выгодно, там задержки получаются маленькими 1...3 нс. Но это не имеет смысла, и поэтому возможно и будет смысл применения 3И-НЕ, с целью уменьшения количества микросхем и как следствие сокращения потребления, всё нужно продумывать, взвешивать все за и против и т. д...
Ну а как ремонтом позанимаюсь, продолжу, на очереди P10.
Дааа... Чувствую сегодня я точно ничего не продолжу, глаза слипаются, голова думать вообще ни о чём не хочет, ноги гудят, напрыгался по табуреткам, по-насверлился, шурупов по-накрутился, по-напилился... Хорошо, что хоть математический аппарат мозга способен ещё просчитывать траекторию руки подносящую бутылку пива ко рту...
Пока сверлил, пилил, думал, пришёл к тому, что всё же придётся полноценно заниматься разработкой, а именно все сигналы выписывать в табличку и указывать сколькими входами каждый нагружен, по мере просчёта и разработки схемы, чтобы своевременно добавлять буферизацию, хорошо хоть с буферами нет проблем, аж два вида, обычных, хоть они и имеют возможность перехода в высокоимпедансное состояние, но тут это не требуется, поэтому вход управления будет тупо идти на землю или Vcc, в зависимости какие будут применяться SV125 или SV126. И задержка стандартная для серии 1,0 нс. Эххх... Пойду пить пиво, отдыхать...
В общим, пойду я дальше заниматься ремонтом и обдумывать, так как вот например, хотелось элементы с большим числом входов, и есть 3И-НЕ (3 input NAND), но он имеет типовую задержку 2,8 нс, что выходит на 0,8 нс медленее, чем если сделать просто составной элемент на 2И-НЕ и ИЛИ, и опять же, нужно рассчитывать схему до конца, так как в младших разрядах, возможно это будет выгодно, там задержки получаются маленькими 1...3 нс. Но это не имеет смысла, и поэтому возможно и будет смысл применения 3И-НЕ, с целью уменьшения количества микросхем и как следствие сокращения потребления, всё нужно продумывать, взвешивать все за и против и т. д...
Ну а как ремонтом позанимаюсь, продолжу, на очереди P10.
Дааа... Чувствую сегодня я точно ничего не продолжу, глаза слипаются, голова думать вообще ни о чём не хочет, ноги гудят, напрыгался по табуреткам, по-насверлился, шурупов по-накрутился, по-напилился... Хорошо, что хоть математический аппарат мозга способен ещё просчитывать траекторию руки подносящую бутылку пива ко рту...
Пока сверлил, пилил, думал, пришёл к тому, что всё же придётся полноценно заниматься разработкой, а именно все сигналы выписывать в табличку и указывать сколькими входами каждый нагружен, по мере просчёта и разработки схемы, чтобы своевременно добавлять буферизацию, хорошо хоть с буферами нет проблем, аж два вида, обычных, хоть они и имеют возможность перехода в высокоимпедансное состояние, но тут это не требуется, поэтому вход управления будет тупо идти на землю или Vcc, в зависимости какие будут применяться SV125 или SV126. И задержка стандартная для серии 1,0 нс. Эххх... Пойду пить пиво, отдыхать...
Viktor2312- RIP
- Сообщения : 15492
Дата регистрации : 2012-08-10
Возраст : 45
Откуда : Пятигорск
 .
.
21
Решил, что нужно начать перечерчивать схему, во-первых с учётом некоторых тонкостей, чисто дизайна, чтобы всё было однотипно и стандартно, отступы там и т. д... Во-вторых, с учётом всех появившихся и выявленных доработок, как то, например, использование буфферизированных сигналов в младших разрядах, где задержка минимальна, и задержка в буфере в +1,0 нс не критична и не важна, то есть 2,0 нс, и оставление на будущие, в более старшие разряды, сигналов с задержкой в 1,0 нс, где составные элементы, для повышения количества входов, просто неизбежны. Сегодня начал, но закончить не успел... Мозг сказал, собирай манатки, пиз... й работать, бабло нужно здесь и сейчас, а все эти... Тут, что-то начал вспоминаться лучший фильм XX века... " - Да ты, какой-то еродиевый... Не знаю... А всё, что ты в голос кричишь... " Не буду развивать тему...
Пока так, что успел с утра, проверка обязательна, но...
Главное теперь веду учёт нагрузки, количество Входов на каждый выход:
Но чувствую ещё ни раз придётся, если не перечерчивать, то дополнять... Хотя нужно двигаться дальше, срочно и интенсивно...
А схема, под спойлер закатаю:
Не забываем всё идёт от 0 (нуля) как и в жизни, вы родились, пошёл нулевой год, движемся в право, в данном конкретном случае, вы же не отмечаете 1 год при рождении, нет, вы родились 0, прожили 1 год, отмечаете 1 годик и т. д... Так и тут главное от нуля, но и есть извращение с направлением, но оно сейчас не важно...
...
Пока так, что успел с утра, проверка обязательна, но...
Главное теперь веду учёт нагрузки, количество Входов на каждый выход:
Но чувствую ещё ни раз придётся, если не перечерчивать, то дополнять... Хотя нужно двигаться дальше, срочно и интенсивно...
А схема, под спойлер закатаю:
- Спойлер:
Не забываем всё идёт от 0 (нуля) как и в жизни, вы родились, пошёл нулевой год, движемся в право, в данном конкретном случае, вы же не отмечаете 1 год при рождении, нет, вы родились 0, прожили 1 год, отмечаете 1 годик и т. д... Так и тут главное от нуля, но и есть извращение с направлением, но оно сейчас не важно...
...
Viktor2312- RIP
- Сообщения : 15492
Дата регистрации : 2012-08-10
Возраст : 45
Откуда : Пятигорск
 .
.
22
Эхх... Чем дальше в лес, тем больше дров. И в правду. Сегодня опять просматривая расчёты и обдумывая всякое разное, обратил внимание на то, что очень многие сигналы, повторяются в последующих разрядах, то есть по сути начинается дублирование. Что приводит к тому, что можно их брать из предыдущих разрядов. Стало это возможным из-за составных элементов, так как нет многовходовых элементов и они составляются из элементов с меньшим количеством входов, но тем самым появляется доступ к сигналам, которые обычно находятся внутри микросхем и не доступны для вывода наружу. Это хорошо, так как позволит уменьшить количество логических элементов. Но схему опять придётся перечерчивать. Хотя в этот раз, я думаю лучше довести расчёты до конца с вычерчиванием кусочков схем, так как их приходится модернизировать порой до вообще одного логического элемента, как вот например вышло при расчёте бита переноса P8. Часть схемы стала такой:
Как видно из формулы, это по сути элемент 6И-НЕ, который у нас трансформировался всего до одного логического элемента 2ИЛИ, из-за того, что все остальные сигналы мы уже получали в предыдущих разрядах и нет смысла создавать полную схему составного логического элемента 6И-НЕ, достаточно взять уже полученные сигналы, главное только следить за нагрузочной способностью.
Ладно, у меня ремонт в процессе, я по сути не думаю, а пилю, сверлю рейки и стены, а сейчас вообще нужно идти за шурупами, гвоздиками и пеноплэксом, как на нём написано, тупость, почему не назвать пеноплексом... Да и пивка хочется бутылочку заточить, пока таньга есть, а то мои 1050 вообще за последние трое суток аж на 1500 настарались, жаль что так не всегда, хотя...
Печаль, печаль... На данный момент я точно пришёл к выводу, что на данном этапе, я не смогу применить КТО, СОК и АМ. Вся проблема в преобразовании из ПСС изначальной (ПСС - позиционная система счисления) в СОК и обратно. Сам процесс преобразования больше времени сожрёт, чем выхлоп при сложении, пусть и 5-ти битных величин и параллельно, но... Нужно рассмотреть другие не позиционные системы, их много, хотя боюсь вот это преобразование туда обратно, сведёт всё на нет, а проблема в том, что много битовых и операций сдвига, и тут придётся из СОК возвращать в ПСС. Поэтому пока вариант только один, в этой версии, параллельный сумматор с параллельным переносом, и как вроде пока всё классно развивается, именно благодаря составным элементам...
Как видно из формулы, это по сути элемент 6И-НЕ, который у нас трансформировался всего до одного логического элемента 2ИЛИ, из-за того, что все остальные сигналы мы уже получали в предыдущих разрядах и нет смысла создавать полную схему составного логического элемента 6И-НЕ, достаточно взять уже полученные сигналы, главное только следить за нагрузочной способностью.
Ладно, у меня ремонт в процессе, я по сути не думаю, а пилю, сверлю рейки и стены, а сейчас вообще нужно идти за шурупами, гвоздиками и пеноплэксом, как на нём написано, тупость, почему не назвать пеноплексом... Да и пивка хочется бутылочку заточить, пока таньга есть, а то мои 1050 вообще за последние трое суток аж на 1500 настарались, жаль что так не всегда, хотя...
Печаль, печаль... На данный момент я точно пришёл к выводу, что на данном этапе, я не смогу применить КТО, СОК и АМ. Вся проблема в преобразовании из ПСС изначальной (ПСС - позиционная система счисления) в СОК и обратно. Сам процесс преобразования больше времени сожрёт, чем выхлоп при сложении, пусть и 5-ти битных величин и параллельно, но... Нужно рассмотреть другие не позиционные системы, их много, хотя боюсь вот это преобразование туда обратно, сведёт всё на нет, а проблема в том, что много битовых и операций сдвига, и тут придётся из СОК возвращать в ПСС. Поэтому пока вариант только один, в этой версии, параллельный сумматор с параллельным переносом, и как вроде пока всё классно развивается, именно благодаря составным элементам...
Viktor2312- RIP
- Сообщения : 15492
Дата регистрации : 2012-08-10
Возраст : 45
Откуда : Пятигорск
Viktor2312- RIP
- Сообщения : 15492
Дата регистрации : 2012-08-10
Возраст : 45
Откуда : Пятигорск
 .
.
25
Пошёл, пошёл, пошёл процесс потихоньку...
Это ver0.01 и то разработка модуля Sum_0, если выше по теме посмотреть, то всё будет понятно A делаем rotr2 и rotr13 потом складываем по модулю два, и делаем с A rotr22 и снова складываем с результатом предыдущего сложения, циклические сдвиги мы делаем физически за 0,0 нс, а сложение по модулю два, то бишь "Исключающее ИЛИ" логически, на логических элементах. Так как с первой итерации A нам уже не известно, то потребуется 63 таких модуля для оставшихся итераций первого раунда и потом 63 для второго, всего 126 идентичных модулей, ну и 0,6 нс на два это максимум чего можно добиться при -40оС то есть 1,2 нс и 4,0 нс на два, при +85оС и хорошем монтаже, то есть 8,0 нс, типовое значение 2,0 нс, на которое я рассчитываю.
Размеры модуля 75 х 75 мм (7,5 х 7,5 см) связано чисто с входным и выходным разъёмом, в 7,0 х 7,0 см чуть не укладываюсь, да и вообще не укладываюсь, можно конечно перейти на следующий уровень в производстве печатных плат и тогда точно укладываюсь в 7 см квадратик, но для прототипа, это будет дорого, итак дорого, а GPU еле шевелятся по 1,5к руб за три дня, да 1050, да древность из 2016 года, но пока ковыряют, нужно ускоряться...
Так скрин, же:

Вторую сторону не показываю, лень, там эти пустоты, заполнены вертикальными дорожками, да и разведено чуть больше 1/3 сигналов. Я кстати схему даже не вычертил, потом вычерчу по плате, так как итак всё понятно, из выше изложенной и проработанной информации.
В общим, всё очень сложно и геморойно, если честно, так-то как вроде да вон фигня, а доходит до нюансов и тонкостей, и начинается... Иногда руки просто опускаются, но, уже и во сне разрабатываю, нужно ковырять дальше...
Это ver0.01 и то разработка модуля Sum_0, если выше по теме посмотреть, то всё будет понятно A делаем rotr2 и rotr13 потом складываем по модулю два, и делаем с A rotr22 и снова складываем с результатом предыдущего сложения, циклические сдвиги мы делаем физически за 0,0 нс, а сложение по модулю два, то бишь "Исключающее ИЛИ" логически, на логических элементах. Так как с первой итерации A нам уже не известно, то потребуется 63 таких модуля для оставшихся итераций первого раунда и потом 63 для второго, всего 126 идентичных модулей, ну и 0,6 нс на два это максимум чего можно добиться при -40оС то есть 1,2 нс и 4,0 нс на два, при +85оС и хорошем монтаже, то есть 8,0 нс, типовое значение 2,0 нс, на которое я рассчитываю.
Размеры модуля 75 х 75 мм (7,5 х 7,5 см) связано чисто с входным и выходным разъёмом, в 7,0 х 7,0 см чуть не укладываюсь, да и вообще не укладываюсь, можно конечно перейти на следующий уровень в производстве печатных плат и тогда точно укладываюсь в 7 см квадратик, но для прототипа, это будет дорого, итак дорого, а GPU еле шевелятся по 1,5к руб за три дня, да 1050, да древность из 2016 года, но пока ковыряют, нужно ускоряться...
Так скрин, же:

Вторую сторону не показываю, лень, там эти пустоты, заполнены вертикальными дорожками, да и разведено чуть больше 1/3 сигналов. Я кстати схему даже не вычертил, потом вычерчу по плате, так как итак всё понятно, из выше изложенной и проработанной информации.
В общим, всё очень сложно и геморойно, если честно, так-то как вроде да вон фигня, а доходит до нюансов и тонкостей, и начинается... Иногда руки просто опускаются, но, уже и во сне разрабатываю, нужно ковырять дальше...
Viktor2312- RIP
- Сообщения : 15492
Дата регистрации : 2012-08-10
Возраст : 45
Откуда : Пятигорск
Страница 1 из 2 • 1, 2 
 Похожие темы
Похожие темы» БВС-1. Наработки, но не вошедшие в проект в полном виде.
» Разные видео с pro-blockchain.
» Эмуляторы, всякие и разные...
» Монеты разные, новые и старые...
» Всякие разные разговоры про Dizzy-Age
» Разные видео с pro-blockchain.
» Эмуляторы, всякие и разные...
» Монеты разные, новые и старые...
» Всякие разные разговоры про Dizzy-Age
Страница 1 из 2
Права доступа к этому форуму:
Вы не можете отвечать на сообщения|
|
|